题目内容
14.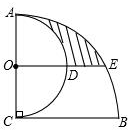 如图,AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作⊙C,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$.
如图,AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作⊙C,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$.
分析 如图,图中S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE.根据已知条件易求得OA=OC=OD=2,BC=CE=4.∠ECB=∠OEC=30°,所以由扇形面积公式、三角形面积公式进行解答即可.
解答 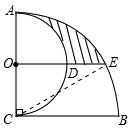 解:如图,连接CE.
解:如图,连接CE.
∵AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{AB}$,
∴∠ACB=90°,OA=OC=OD=1,BC=CE=2.
又∵OE∥BC,
∴∠AOE=∠COE=90°.
∴在直角△OEC中,OC=$\frac{1}{2}$CE,
∴∠OEC=30°,OE=$\sqrt{3}$.
∴∠ECB=∠OEC=30°,
∴S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE
=$\frac{90π×{2}^{2}}{360}$-$\frac{90π×{1}^{2}}{360}$-$\frac{30π×{2}^{2}}{360}$-$\frac{1}{2}$×1×$\sqrt{3}$
=$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$.
故答案为$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$.
点评 本题考查了扇形面积的计算.不规则图形的面积一定要注意分割成规则图形的面积进行计算.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
19.“节能环保,低碳生活”是我们倡导的一种生活方式.某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台.三种家电的进价及售价如表所示:
(1)设购进x台电视机,若购进电视机的数量和洗衣机的数量相同,设销售总额为y元,试求出y元关于x台的函数关系式.
(2)在(1)的条件下,如果不超出现有资金,空调的数量不超过电视机数量的三倍,请问商场有哪几种进货方案?
(3)在“2013年消费促进月”促销活动期间,商家针对这三种节能型产品推出“现金购满1000元送50元家电消费券一张、多买多送”的活动,根据(2)的方案,若三种电器在活动期间全部售出,商家预计最多送出消费券多少张?
| 进价(元/台) | 售价(元/台) | |
| 电视机 | 5000 | 5500 |
| 洗衣机 | 2000 | 2160 |
| 空 调 | 2400 | 2700 |
(2)在(1)的条件下,如果不超出现有资金,空调的数量不超过电视机数量的三倍,请问商场有哪几种进货方案?
(3)在“2013年消费促进月”促销活动期间,商家针对这三种节能型产品推出“现金购满1000元送50元家电消费券一张、多买多送”的活动,根据(2)的方案,若三种电器在活动期间全部售出,商家预计最多送出消费券多少张?

 在六边形ABCDEF中,AF∥CD,∠A=∠D,∠B=∠E,那么BC∥EF吗?为什么?
在六边形ABCDEF中,AF∥CD,∠A=∠D,∠B=∠E,那么BC∥EF吗?为什么?