题目内容
5. 如图,△ABC中,D、E分别是BC、CA上两点,连接AD、BE交于O点,且满足BD=2DC,BO=4OE,求AO:OD.
如图,△ABC中,D、E分别是BC、CA上两点,连接AD、BE交于O点,且满足BD=2DC,BO=4OE,求AO:OD.
分析 作DH∥BE交AC于H,根据平行线分线段成比例定理得到$\frac{DH}{BE}$=$\frac{CD}{CB}$=$\frac{1}{3}$,根据平行线分线段成比例定理求出$\frac{AO}{AD}$=$\frac{OE}{OH}$=$\frac{3}{5}$,得到答案.
解答 解: 作DH∥BE交AC于H,
作DH∥BE交AC于H,
则$\frac{DH}{BE}$=$\frac{CD}{CB}$=$\frac{1}{3}$,
∵BO=4OE,
∴$\frac{OE}{OH}$=$\frac{3}{5}$,
∵DH∥BE,
∴$\frac{AO}{AD}$=$\frac{OE}{OH}$=$\frac{3}{5}$,
∴AO:OD=3:2.
点评 本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列各数:5.9、-2$\frac{1}{3}$、-7、0、$\frac{12}{5}$、8中,正分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.若一个数与它的相反数在数轴上对应点之间的距离为4,则这个数是( )
| A. | -2 | B. | 2 | C. | ±2 | D. | ±4 |
14.二元一次方程x+y=8的一个解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$ |
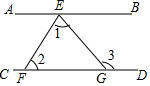 如图,AB∥CD,E是直线AB上的一点,F,G分别是直线CD上的两点,试说明∠3=∠1+∠2.
如图,AB∥CD,E是直线AB上的一点,F,G分别是直线CD上的两点,试说明∠3=∠1+∠2.