题目内容
19.解分式方程:(1)$\frac{2-x}{x-3}$+$\frac{1}{3-x}$-1=0;
(2)$\frac{x+1}{x-1}$-$\frac{4}{{x}^{2}-1}$=1.
分析 方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答 解:(1)$\frac{2-x}{x-3}$+$\frac{1}{3-x}$-1=0,
方程两边同乘以(x-3)得,2-x-1-x+3=0,
解得:x=2,
检验:当x=2时,x-3≠0,
故x=2是原分式方程的解.
(2)$\frac{x+1}{x-1}$-$\frac{4}{{x}^{2}-1}$=1,
两边同乘(x+1)(x-1)得,(x+1)2-4=(x+1)(x-1),
解得,x=-4,
检验:当x=-4时,(x+1)(x-1)≠0,
故x=-4是原分式方程的解.
点评 本题考查了解分式方程:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.

练习册系列答案
相关题目
11.下列运算正确的是( )
| A. | 5ab-3ab=2 | B. | x3n÷xn=x3 | C. | (a-b)2=a2-b2 | D. | (-2x2)3=-8x6 |
 如图,D是AB中点,且CB=CD,E为△ABC外一点,满足CE=CA,过点B作BF⊥BC交EA延长线于E.求证:∠FDA=∠BEA.
如图,D是AB中点,且CB=CD,E为△ABC外一点,满足CE=CA,过点B作BF⊥BC交EA延长线于E.求证:∠FDA=∠BEA.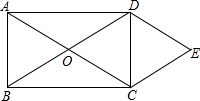 如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证: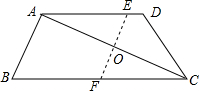 如图,在四边形ABCD中,AD∥BC,把四边形对折,使点A、C重合,折痕EF分别交AD于点E,交BC于点F.
如图,在四边形ABCD中,AD∥BC,把四边形对折,使点A、C重合,折痕EF分别交AD于点E,交BC于点F.