Question

8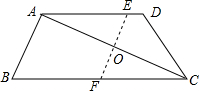．如图，在四边形ABCD中，AD∥BC，把四边形对折，使点A、C重合，折痕EF分别交AD于点E，交BC于点F．
（1）求证：△AOE≌△COF．
（2）说明：点E与F关于直线AC对称．

Answer 1

分析 （1）根据平行线的性质得到∠DAC=∠BCA，根据翻转变换的性质得到OA=OC，根据全等三角形的判定定理证明即可；
（2）根据全等三角形的性质得到OE=OF，根据轴对称的性质证明．

解答 （1）证明：∵AD∥BC，
∴∠DAC=∠BCA，
∵把四边形沿EF对折，点A、C重合，
∴OA=OC，AC⊥EF，
在△AOE和△COF中，
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$
∴△AOE≌△COF；
（2）证明：∵△AOE≌△COF，
∴OE=OF，又AC⊥EF，
∴点E与F关于直线AC对称．

点评 本题考查的是翻转变换的性质、全等三角形的判定和性质、轴对称的性质，掌握翻转变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．