题目内容
14.Rt△ABC中,∠C=90°,AC=3,BC=4,则中线CD的长是( )| A. | 2 | B. | 2.5 | C. | 5 | D. | 1.5 |
分析 根据勾股定理求出AB的长,根据直角三角形的性质计算即可.
解答 解:∵∠C=90°,AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∴CD=$\frac{1}{2}$AB=2.5,
故选:B.
点评 本题考查的是直角三角形的性质和勾股定理,直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
5.若一组数据1,2,x,4的众数是1,则这组数据的方差为( )
| A. | 1 | B. | 2 | C. | 1.5 | D. | $\sqrt{2}$ |
2.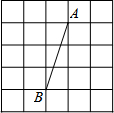 如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数有( )
如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数有( )
 如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数有( )
如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数有( )| A. | 4个 | B. | 6个 | C. | 8个 | D. | 10个 |
6.已知:⊙O的直径等于4,点P到圆心O的长度OP=4,则点P与⊙O的位置关系为( )
| A. | P在⊙O上 | B. | P在⊙O内 | C. | P在⊙O外 | D. | 不确定 |
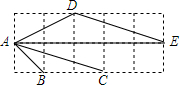 如图,在5×2的正方形网格中,小正方形的边长为1,△ABC与△ADE的顶点都在格点上.
如图,在5×2的正方形网格中,小正方形的边长为1,△ABC与△ADE的顶点都在格点上.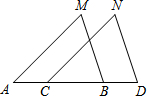 如图,已知A、B、C、D在同一直线上,AM=CN,MA∥NC,∠M=∠N,证明:AC=BD.
如图,已知A、B、C、D在同一直线上,AM=CN,MA∥NC,∠M=∠N,证明:AC=BD.