题目内容
10.抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C(0,4),且点B的坐标为(-4,0),点A在原点和点B之间,则a的取值范围是a>$\frac{1}{4}$.分析 把B、C两点坐标代入抛物线解得b=4a+1,c=4,再根据-4<-$\frac{b}{2a}$<O,解不等式即可.
解答 解:由题意:$\left\{\begin{array}{l}{c=4}\\{16a-4b+c=0}\end{array}\right.$解得$\left\{\begin{array}{l}{b=4a+1}\\{c=4}\end{array}\right.$,
∴抛物线为y=ax2+(4a+1)x+4,
∵点A在原点和点B之间,
∴-4<-$\frac{4a+1}{2a}$<0,
解得:a>$\frac{1}{4}$,
故答案为a>$\frac{1}{4}$.
点评 本题考查抛物线与x轴的交点,学会用待定系数法求出抛物线的解析式(含有字母a),再根据对称轴的位置列出不等式解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
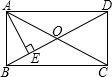 如图,在矩形ABCD中,AE⊥BD,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数.
如图,在矩形ABCD中,AE⊥BD,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数. 如图所示,这三种卡片的数量分别有3张,2张,1张,请你用它们拼出一些长方形或正方形,要求每种卡片都要用到,卡片之间不重叠,并用两种不同的方式计算它的面积.
如图所示,这三种卡片的数量分别有3张,2张,1张,请你用它们拼出一些长方形或正方形,要求每种卡片都要用到,卡片之间不重叠,并用两种不同的方式计算它的面积. 如图,在?ABCD中,AE⊥BD于点E,CF⊥BD于点F,G、H分别为AD、BC的中点.求证:EF、GH互相平分.
如图,在?ABCD中,AE⊥BD于点E,CF⊥BD于点F,G、H分别为AD、BC的中点.求证:EF、GH互相平分. 如图所示,正方形ABCD的边长为2,点E、F分别为边AB、AD 的中点,点G是CF上的一点,使得3CG=2GF,则三角形BEG的面积为$\frac{4}{5}$.
如图所示,正方形ABCD的边长为2,点E、F分别为边AB、AD 的中点,点G是CF上的一点,使得3CG=2GF,则三角形BEG的面积为$\frac{4}{5}$.