题目内容
7. 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为$\frac{2π}{3}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为$\frac{2π}{3}$.
分析 连接OD,则根据垂径定理可得出CE=DE,继而将阴影部分的面积转化为扇形OBD的面积,代入扇形的面积公式求解即可.
解答 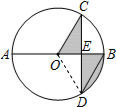 解:连接OD.
解:连接OD.
∵CD⊥AB,
∴CE=DE=$\frac{1}{2}$CD=$\sqrt{3}$(垂径定理),
故S△OCE=S△ODE,
即可得阴影部分的面积等于扇形OBD的面积,
又∵∠CDB=30°,
∴∠COB=60°(圆周角定理),
∴OC=2,
故S扇形OBD=$\frac{60π×{2}^{2}}{360}$=$\frac{2π}{3}$,即阴影部分的面积为$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 此题考查了扇形的面积计算、垂径定理及圆周角定理,解答本题关键是根据图形得出阴影部分的面积等于扇形OBD的面积,另外要熟记扇形的面积公式.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
17.一次函数y=2x-2的图象与y轴的交点坐标是( )
| A. | (-2,0) | B. | (2,0) | C. | (0,-2) | D. | (0,2) |

 解一元一次方程的过程就是通过变形,把一元一次方程转化为x=a的形式.下面是解方程$\frac{2x-0.3}{0.5}-\frac{x+0.4}{0.3}=1$的主要过程,请在如图的矩形框中选择与方程变形对应的依据,并将它前面的序号填入相应的括号中.
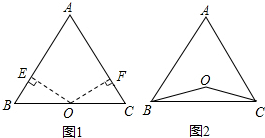
解一元一次方程的过程就是通过变形,把一元一次方程转化为x=a的形式.下面是解方程$\frac{2x-0.3}{0.5}-\frac{x+0.4}{0.3}=1$的主要过程,请在如图的矩形框中选择与方程变形对应的依据,并将它前面的序号填入相应的括号中. 如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=5,则△BCE的面积为5.
如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=5,则△BCE的面积为5.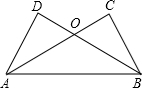 如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,若AC=5,BO=3,则OD=2.
如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,若AC=5,BO=3,则OD=2.