题目内容
13.已知抛物线y=x2-2(k-1)x+k2-7与x轴有两个不同的公共点,求k的取值范围.分析 首先确定a、b、c的值,抛物线与x轴有两个不同交点,则△=b2-4ac>0,即可即可列不等式求解.
解答 解:a=1,b=-2(k-1),c=k2-7,
△=4(k-1)2-4(k2-7)>0,
即-8k+32>0,
解得:k<4.
点评 本题考查了二次函数与x轴交点的个数的判断,当△>0时,有两个不同交点,当△=0时有一个交点,即顶点在x轴上,当△<0时,没有公共点.

练习册系列答案
相关题目
1.下列图形中,形如中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.下列运算中没有意义的是( )
| A. | -2006÷[(-$\frac{7}{3}$)×3+7] | B. | [(-$\frac{7}{3}$)×3+7]÷(-2006) | C. | ($\frac{1}{3}$-$\frac{1}{2}$)÷[0-(-4)]×(-2) | D. | 2$\frac{1}{3}$÷(3$\frac{1}{3}$×6-18) |
 已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.
已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.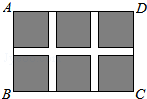 如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?
如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?