题目内容
如图,等腰直角△ABC中AB=AC,将其按下图所示的方式折叠两次,

若DA’=1,给出下列说法:①DC’平分∠BDA’;②BA’长为 ;③△BC’D是等腰三角形;④△CA’D的周长等于BC的长.其中正确的有
;③△BC’D是等腰三角形;④△CA’D的周长等于BC的长.其中正确的有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:本题是等腰直角三角形的折叠问题,由于AB=AC,所以∠B=∠C=45°,两次折叠后,有许多相等的量,利用这些条件结合勾股定理可得出正确答案.
解答:∵等腰直角△ABC中,∴AB=AC
∴∠B=∠C=45°
∵折叠
∴DA'⊥BC,DA=DA',AB=BA'DC=DC',∠DC'C=∠C=45°,∠DBC'= ∠ABC=
∠ABC= ×45°=22.5°,C'A'=CA'
×45°=22.5°,C'A'=CA'
∴∠BDC'=∠DC'C-∠DBC'=45°-22.5°=22.5°=∠DBC'
∴BC'=DC',
∴△BC’D是等腰三角形
Rt△DA'C中,∠C=45°,∴∠A'DC=90°-45°=45°
∴A'C=A'D=1,∴CD= =
=
∴BC'=
BA'=BC'+C'A'= +1
+1
△CA’D的周长等于CD+CA'+DA'=DC'+C'A'+CA'=BC'+C'A'+CA'=BC
∠BDC'=22.5°.∠C'DA'=45°
∴DC’不平分∠BDA’
∴①错误,②,③,④正确,故选C.
点评:折叠问题要注意在图形上找条件,由于折叠,会有许多相等的边,角,对我们做题都是有帮助的.
分析:本题是等腰直角三角形的折叠问题,由于AB=AC,所以∠B=∠C=45°,两次折叠后,有许多相等的量,利用这些条件结合勾股定理可得出正确答案.
解答:∵等腰直角△ABC中,∴AB=AC
∴∠B=∠C=45°
∵折叠
∴DA'⊥BC,DA=DA',AB=BA'DC=DC',∠DC'C=∠C=45°,∠DBC'=
 ∠ABC=
∠ABC= ×45°=22.5°,C'A'=CA'
×45°=22.5°,C'A'=CA'∴∠BDC'=∠DC'C-∠DBC'=45°-22.5°=22.5°=∠DBC'
∴BC'=DC',
∴△BC’D是等腰三角形
Rt△DA'C中,∠C=45°,∴∠A'DC=90°-45°=45°
∴A'C=A'D=1,∴CD=
 =
=
∴BC'=

BA'=BC'+C'A'=
 +1
+1△CA’D的周长等于CD+CA'+DA'=DC'+C'A'+CA'=BC'+C'A'+CA'=BC
∠BDC'=22.5°.∠C'DA'=45°
∴DC’不平分∠BDA’
∴①错误,②,③,④正确,故选C.
点评:折叠问题要注意在图形上找条件,由于折叠,会有许多相等的边,角,对我们做题都是有帮助的.

练习册系列答案
相关题目
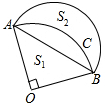 如图,等腰直角三角形AOB的面积为S1,以点O为圆心,OA为半径的弧与以AB为直径的半圆围成的图形的面积为S2,则S1与S2的关系是( )
如图,等腰直角三角形AOB的面积为S1,以点O为圆心,OA为半径的弧与以AB为直径的半圆围成的图形的面积为S2,则S1与S2的关系是( )| A、S1>S2 | B、S1<S2 | C、S1=S2 | D、S1≥S2 |
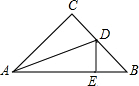 如图,等腰直角三角形ABC中,∠C=90°,AD为∠CAB的平分线,DE⊥AB于E,AC=4,则△BDE的周长为( )
如图,等腰直角三角形ABC中,∠C=90°,AD为∠CAB的平分线,DE⊥AB于E,AC=4,则△BDE的周长为( )| A、4 | ||
| B、6 | ||
C、4
| ||
D、4
|
 (2012•镇江模拟)如图,等腰直角三角形ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( )
(2012•镇江模拟)如图,等腰直角三角形ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( ) 如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE.
如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE. 如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.
如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.