题目内容
已知,在平面直角从标系中,A点坐标为(0,4),B点坐标为(2,0),C(m,6)为反比例函数
 图象上一点.将△AOB绕B点旋转至△A′O′B处.
图象上一点.将△AOB绕B点旋转至△A′O′B处.
(1)求m的值;
(2)若O′落在OC上,连接AA′交OC与D点.①求证:四边形ACA′O′为平行四边形; ②求CD的长度;
(3)直接写出当AO′最短和最长时A′点的坐标.


【考点】反比例函数综合题;等边三角形的判定与性质;平行四边形的判定与性质;相似三角形的判定与性质;特殊角的三角函数值.
【专题】综合题.
【分析】(1)只需把点C的坐标代入反比例函数的解析式,就可解决问题;
(2)①过点C作CH⊥y轴与H,如图1,易证AC=OA=O′A′,要证四边形ACA′O′为平行四边形,只需证AC∥O′A′,只需证∠ACO=∠A′O′C即可;
②由平行四边形ACA′O′可得CD=
 CO′,要求CD,只需求CO′,只需求出OC及OO′即可;
CO′,要求CD,只需求CO′,只需求出OC及OO′即可;
(3)根据两点之间线段最短可知:当点O′在线段AB上时AO′最短(如图2),当点O′在线段AB的延长线上时AO′最长(如图3);过点O′作O′N⊥x轴于N,过点A′作A′M⊥O′N于M,易证△BNO′∽△BOA,△A′MO′∽△O′NB,然后只需运用相似三角形的性质即可解决问题.
【解答】解:(1)∵C(m,6)为反比例函数
 图象上一点,
图象上一点,
∴m=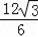
 =2
=2
 ;
;
(2)①过点C作CH⊥y轴与H,如图1.


∵点C的坐标为(2
 ,6),
,6),
∴CH=2
 ,OH=6,
,OH=6,
∴tan∠COH=
 =
=
 ,AC=
,AC=
 =4,
=4,
∴∠COH=30°,OA=AC,
∴∠BOO′=60°,∠ACO=∠AOC=30°.
∵BO′=BO,
∴∠BO′O=∠BOO′=60°.
∵∠A′O′B=∠AOB=90°,
∴∠CO′A′=30°,
∴∠ACO=∠CO′A′,
∴AC∥O′A′.
又∵O′A′=OA=AC,
∴四边形ACA′O′为平行四边形;
②∵BO′=BO,∠BOO′=60°,
∴△BOB′是等边三角形,
∴OO′=OB=2.
∵∠CHO=90°,CH=2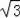
 ,OH=6,
,OH=6,
∴OC=4
 ,
,
∴CO′=OC﹣OO′=4
 ﹣2.
﹣2.
∵四边形ACA′O′为平行四边形,
∴CD=O′D=
 CO′=2
CO′=2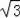
 ﹣1;
﹣1;
(3)当AO′最短时A′点的坐标(2+
 ,
,
 ),当AO′最长时A′点的坐标(2﹣
),当AO′最长时A′点的坐标(2﹣
 ,﹣
,﹣
 ).
).
提示:①当点O′在线段AB上时,AO′最短,
过点O′作O′N⊥x轴于N,过点A′作A′M⊥O′N于M,如图2.


∵O′N∥OA,
∴△BNO′∽△BOA,
∴
 =
=
 =
=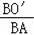
 ,
,
∴
 =
=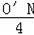
 =
=
 ,
,
∴BN=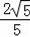
 ,O′N=
,O′N=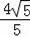
 .
.
∵∠A′MO′=∠A′O′B=∠O′NB=90°,
∴∠MA′O′=∠NO′B,
∴△A′MO′∽△O′NB,
∴
 =
=
 =2,
=2,
∴A′M=
 ,O′M=
,O′M=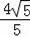
 ,
,
∴A′(2﹣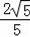
 +
+
 ,
,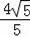
 +
+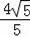
 )即(2+
)即(2+
 ,
,
 );
);
②当点O′在线段AB延长线上时,AO′最长,
过点O′作O′N⊥x轴于N,过点A′作A′M⊥O′N于M,如图3.


同理可得:A′(2﹣
 ,﹣
,﹣
 ).
).
【点评】本题主要考查了反比例函数图象上点的坐标特征、旋转的性质、相似三角形的判定与性质、平行四边形的判定与性质、等边三角形的判定与性质、三角函数的定义、特殊角的三角函数值、勾股定理等知识,利用平行四边形的对角线互相平分是解决第(2)②小题的关键,构造K型相似是解决第(3)小题的关键.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案


 ﹣1=
﹣1=
 的解集是( )
的解集是( )




