题目内容
如图正方形ABCD,其边长为4.P是射线AB上的点,且AP=x.将△APD沿过点D的折痕PD折叠,点A的落点记为A′,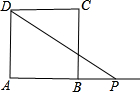 若△A′DP与正方形ABCD的重叠面积记为S,
若△A′DP与正方形ABCD的重叠面积记为S,
(1)若x=6,则S=______
(2) ≤S≤1时,则x的取值范围为(用含x的不等式表示)______.
≤S≤1时,则x的取值范围为(用含x的不等式表示)______.
解:(1)设PD和BC的交点为E,如下图所示:
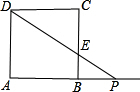
由题意可知,△A′DP与正方形ABCD的重叠部分的面积即是△CDE的面积.
AP=6,AB=4,∴BP=2,
又△DCE∽△PBE,
∴ =
= =
= ,
,
又BE+CE=4,
∴CE= ,
,
S△CDE= ×
× ×4=
×4= .
.
(2)当点P在AB之间时,△A′DP与正方形ABCD的重叠面积即是求△A′DP的面积,
∴S= ×4×x=2x,
×4×x=2x,
又 ≤S≤1,
≤S≤1,
解得: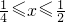 ;
;
当点P在点B的右端时,△A′DP与正方形ABCD的重叠部分的面积即是△CDE的面积,
∴S=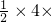
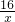 =
=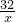 ,
,
又 ≤S≤1,
≤S≤1,
解得:32≤x≤64.
故答案为: ;
;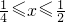 或32≤x≤64.
或32≤x≤64.
分析:设PD和BC的交点为E,由题意可知,△A′DP与正方形ABCD的重叠部分的面积即是△CDE的面积.
(1)AP=6,AB=4,所以BP=2,又△DCE∽△PBE,即可求出CE的长,从而求出其面积.
(2)分两种情况讨论,①点P在AB之间,②点P在点B的右端,分别写出这两种情况下重叠面积的表达式,然后计算即可.
点评:本题考查了翻转变换、三角形的面积、直角三角形和正方形的性质等知识,有一定难度,需要熟练掌握各部分知识,注意第二问中不要漏解.

由题意可知,△A′DP与正方形ABCD的重叠部分的面积即是△CDE的面积.
AP=6,AB=4,∴BP=2,
又△DCE∽△PBE,
∴
 =
= =
= ,
,又BE+CE=4,
∴CE=
 ,
,S△CDE=
 ×
× ×4=
×4= .
.(2)当点P在AB之间时,△A′DP与正方形ABCD的重叠面积即是求△A′DP的面积,
∴S=
 ×4×x=2x,
×4×x=2x,又
 ≤S≤1,
≤S≤1,解得:
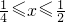 ;
;当点P在点B的右端时,△A′DP与正方形ABCD的重叠部分的面积即是△CDE的面积,
∴S=
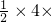
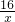 =
=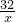 ,
,又
 ≤S≤1,
≤S≤1,解得:32≤x≤64.
故答案为:
 ;
;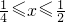 或32≤x≤64.
或32≤x≤64.分析:设PD和BC的交点为E,由题意可知,△A′DP与正方形ABCD的重叠部分的面积即是△CDE的面积.
(1)AP=6,AB=4,所以BP=2,又△DCE∽△PBE,即可求出CE的长,从而求出其面积.
(2)分两种情况讨论,①点P在AB之间,②点P在点B的右端,分别写出这两种情况下重叠面积的表达式,然后计算即可.
点评:本题考查了翻转变换、三角形的面积、直角三角形和正方形的性质等知识,有一定难度,需要熟练掌握各部分知识,注意第二问中不要漏解.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图正方形ABCD的边长为2cm,O是AB的中点,也是抛物线的顶点,OP⊥AB,两半圆的直径分别为OA与OB.抛物线经过C、D两点,且关于OP对称,则图中阴影部分的面积之和为
如图正方形ABCD的边长为2cm,O是AB的中点,也是抛物线的顶点,OP⊥AB,两半圆的直径分别为OA与OB.抛物线经过C、D两点,且关于OP对称,则图中阴影部分的面积之和为 25、如图正方形ABCD的边CD上有一点E,连接AE,以A为圆心,AE长为半径画弧,交CB的延长线于F,证明△ADE≌△ABF.
25、如图正方形ABCD的边CD上有一点E,连接AE,以A为圆心,AE长为半径画弧,交CB的延长线于F,证明△ADE≌△ABF. 点F.
点F. 如图,如图正方形ABCD内一点E,满足△CDE为正三角形,直线AE交BC于F点,过E点的直线GH⊥AF,交AB于点G,交CD于点H.以下结论:
如图,如图正方形ABCD内一点E,满足△CDE为正三角形,直线AE交BC于F点,过E点的直线GH⊥AF,交AB于点G,交CD于点H.以下结论: (2013•鄂州)如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
(2013•鄂州)如图正方形ABCD的边长为4,E、F分别为DC、BC中点.