题目内容
20. 已知:如图,AB∥CD,E是AB的中点,CE=DE.
已知:如图,AB∥CD,E是AB的中点,CE=DE. (1)求证:∠AED=∠BEC;
(2)连接AC、BD,求证:AC=BD.
分析 (1)由CE=DE,根据等边对等角可得∠EDC=∠ECD,又AB∥CD,得到∠AED=∠EDC,∠BEC=∠ECD,利用等量代换即可解答.
(2)利用SAS证明△AEC≌△BED,即可得到AC=BD.
解答 解:(1)∵CE=DE,
∴∠EDC=∠ECD,
又∵AB∥CD,
∴∠AED=∠EDC,∠BEC=∠ECD
∴∠AED=∠BEC.
(2)如图,
∵∠AED=∠BEC,
∴∠AEC=∠BED,
∵E是AB的中点,
∴AE=BE
在△AEC和△BED中,
$\left\{\begin{array}{l}{AE=BE}\\{∠AEC=∠BED}\\{CE=DE}\end{array}\right.$,
∴△AEC≌△BED.
∴AC=BD.
点评 本题考查了等腰三角形的性质、全等三角形的性质定理与判定定理,解决本题的关键是证明△AEC≌△BED.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
 如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②③④ |
5.我市2015年某一天的最高气温为8℃,最低气温为-2℃,那么这天的最高气温比最低气温高( )
| A. | -10℃ | B. | -6℃ | C. | 6℃ | D. | 10℃ |
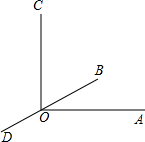 如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′.
如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′. 解不等式2(x+1)-1≥4x+3,并把它的解集在数轴上表示出来.
解不等式2(x+1)-1≥4x+3,并把它的解集在数轴上表示出来.