题目内容
6.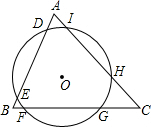 如图,圆心O为△ABC的内心,⊙O截得的弦DE=4cm,则FG=4cm.
如图,圆心O为△ABC的内心,⊙O截得的弦DE=4cm,则FG=4cm.
分析 过O作ON⊥FG于N,OM⊥DE于M,连接OD、OF,根据垂径定理得出DE=2DM,FG=2FN,根据角平分线性质得出OM=ON,根据HL证Rt△OMD≌Rt△ONF,根据全等得出DM=FN,即可求出DE=FG.
解答 解: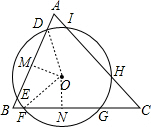
过O作ON⊥FG于N,OM⊥DE于M,连接OD、OF,
则DE=2DM,FG=2FN(垂径定理),∠OMD=∠ONF=90°,OD=OF,
∵O为△ABC的内心,
∴OM=ON,
在Rt△OMD和Rt△ONF中
$\left\{\begin{array}{l}{OD=OF}\\{OM=ON}\end{array}\right.$
∴Rt△OMD≌Rt△ONF(HL),
∴DM=FN,
∵DE=2DM,FG=2FN,
∴FG=DE,
∵DE=4cm,
∴FG=4cm,
故答案为:4.
点评 本题考查了三角形的内切圆,角平分线性质,全等三角形的性质和判定的应用,能求出DE=FG是解此题的关键,注意:角平分线上的点到这个角的两边的距离相等.

练习册系列答案
相关题目
13.-$\frac{1}{8}$的立方根是( )
| A. | -$\frac{1}{2}$ | B. | $±\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
 α B. 90°+
α B. 90°+
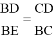 ;③点F是BC的中点;④若
;③点F是BC的中点;④若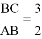 ,则tanE=
,则tanE=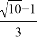 .
. 如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm.
如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm. 下面是从不同方向看用正方块塔建的几何体得到的平面图.
下面是从不同方向看用正方块塔建的几何体得到的平面图. 如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.
如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.