题目内容
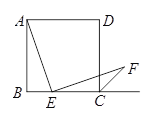
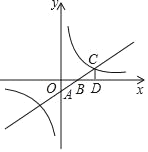
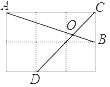
【题目】如图，在边长为1的小正方形网格中，点A，B，C，D都在这些小正方形上，AB与CD相交于点O，则tan∠AOD等于（ ）
A. 
B. 2C. 1D. 
【答案】B
【解析】
连接BE，与CD交于点F，根据正方形的性质可得BF＝CF，证明△ACO∽△BHO，根据相似三角形的性质可得HO：CO=BH：AC=1：3，得到
在Rt△OBF中，求出tan∠BOF=
=2,即可求出tan∠AOD.
解：如图，连接BE，与CD交于点F，
∵四边形BCEH是正方形，
∴
，CH=BE，BE⊥CH，
∴BF＝CF，
∵AC∥BH，
∴△ACO∽△BHO，
∴HO：CO=BH：AC=1：3，
∵CF=HF，
∴HO：HF＝1：2，
∴
在Rt△OBF中，tan∠BOF==2,
∵∠AOD＝∠BOF，
∴tan∠AOD＝2．
故选：B．
练习册系列答案
相关题目
