Question

【题目】综合与探究

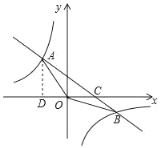
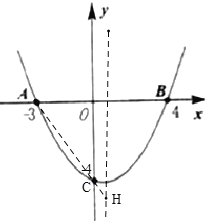
如图，抛物线与轴交于、两点，与轴交于点.

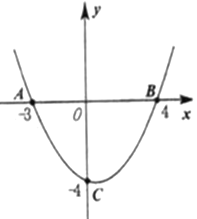
（1）求抛物线解析式：

（2）抛物线对称轴上存在一点，连接、，当值最大时，求点H坐标：

（3）若抛物线上存在一点，，当时，求点坐标：

（4）若点M是平分线上的一点，点是平面内一点，若以、、、为顶点的四边形是矩形，请直接写出点坐标.

Answer 1

【答案】（1）；（2）点；（3）；（4），

【解析】

（1）把A、B两点坐标代入抛物线解析式，解方程组求出a、b的值即可得答案；（2）连接AC，延长AC交抛物线对称轴与H，由A、C两点坐标可得直线AC的解析式，根据抛物线解析式可得对称轴方程，根据A、C、H三点在一条直线时，的值最大，即可得答案；（3）由C点坐标可得△ABC和△ABP的高为4，可得P点纵坐标n=±4，把n=±4代入抛物线解析式求出m的值，根据mn>0即可得P点坐标；（4）设∠BAC的角平分线与y轴交于E点，过点E作EF⊥AC，根据角平分线的性质可证明△AFE≌△AOE，可得出AF的长，利用勾股定理可求出OE的长，可得E点坐标，进而利用待定系数法可求出直线AE的解析式，分两种情况：①当∠ABM1=90°时，M1N1=AB，AN1=BM，M1B⊥x轴，可得点M1的横坐标，代入AE的解析式可得点M1的纵坐标，即可得出BM的长，进而可得N1点坐标；②当∠AM2B=90°时，可知∠N2BA=∠BAE，过N2作N2G⊥x轴，根据点E坐标可得∠BAE的正弦值和余弦值，即可求出BN2的长，利用∠N2BA的正弦和余弦可求出N2G和BG的长，进而可得OG的长，即可得N2坐标；综上即可得答案.

（1）∵A（-3，0），B（4，0），点A、B在抛物线上，

∴

解得：，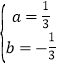

∴抛物线的解析式为：y=x2-x-4.

（2）连接AC，延长AC交抛物线对称轴与H，

∵抛物线解析式为y=x2-x-4，与轴交于点C

∴C（0，-4），对称轴为直线x=-=，

∵≤AC，

∴A、C、H在一条直线上时取最小值，

设直线AC的解析式为y=kx+b,

∴，

解得：，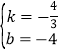

∴直线AC的解析式为y=x-4，

当x=时，y=，

∴H点坐标为（，）.

（3）∵S△ABC=S△ABP，

∴ABOC=AB ，

∴=4，

当n=4时，4=m2-m-4，

解得m=，

∵mn>0，

∴m=，

∴P点坐标为（，4）

当n=-4时，-4=m2-m-4，

解得：m=1或m=0，

∵mn>0，

∴m=1或m=0均不符合题意，

综上：P点坐标为（，4）.

（4）设∠BAC的角平分线交y轴于E，过E作EF⊥AC于F，

∵A（-3，0），B（4，0），C（0，-4），

∴AB=7，AC=5，OA=3，OC=4，

∵AE为∠BAC的角平分线，

∴OE=EF，

又∵AE=AE，

△AOE≌△FAE，

∴AF=OA=3，

∴FC=5-3=2，

∴EF2+FC2=CE2，即OE2+22=(4-OE)2，

解得：OE=，

∵点E在y轴负半轴，

∴E点坐标为（0，-），

设直线AE的解析式为y=kx+b，

∴

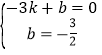
解得：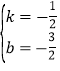

∴直线AE的解析式为y=，

①当∠ABM1=90°时，

∵ANMB是矩形，

∴M1N1=AB=7，AN1=BM，M1B⊥x轴，AN1⊥x轴，

∴x=4时，y=，

∴点N1坐标为（-3，）.

②当∠AM2B=90°时，过N2作N2G⊥x轴，

∵AM2BN2是矩形，

∴∠N2BA=∠BAE，

∵OA=3，OE=，

∴AE=，

∴sin∠BAE==，cos∠BAE==，

∴sin∠N2BA =，cos∠N2BA=

∴BN2=ABcos∠N2BA=，

∴N2G=BN2sin∠N2BA=，BG=BN2cos∠N2BA=，

∴OB-BG=-，

∴点N2坐标为（-，）.

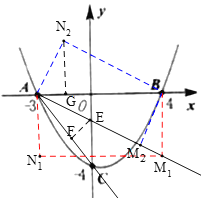
综上所述：点N的坐标为N1（-3，），N2（-，）.