题目内容
9. 在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论:
在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论:①AM=CN;
②∠AME=∠BNE;
③BN-AM=2;
④S△EMN=$\frac{2}{co{s}^{2}α}$.
上述结论中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①作辅助线EF⊥BC于点F,然后证明Rt△AME≌Rt△FNE,从而求出AM=FN,所以BM与CN的长度相等.
②由①Rt△AME≌Rt△FNE,即可得到结论正确;
③经过简单的计算得到BN-AM=BC-CN-AM=BC-BM-AM=BC-(BM+AM)=BC-AB=4-2=2,
④方法一:用面积的和和差进行计算,用数值代换即可.方法二:先判断出△EMN是等腰直角三角形,再用面积公式即可.
解答 解:①如图,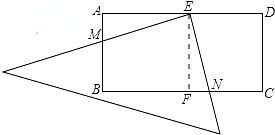
在矩形ABCD中,AD=2AB,E是AD的中点,
作EF⊥BC于点F,则有AB=AE=EF=FC,
∵∠AEM+∠DEN=90°,∠FEN+∠DEN=90°,
∴∠AEM=∠FEN,
在Rt△AME和Rt△FNE中,
$\left\{\begin{array}{l}{∠AEM=∠FEN}\\{AE=EF}\\{∠MAE=∠NFE}\end{array}\right.$,
∴Rt△AME≌Rt△FNE,
∴AM=FN,
∴MB=CN.
∵AM不一定等于CN,
∴①错误,
②由①有Rt△AME≌Rt△FNE,
∴∠AME=∠BNE,
∴②正确,
③由①得,BM=CN,
∵AD=2AB=4,
∴BC=4,AB=2
∴BN-AM=BC-CN-AM=BC-BM-AM=BC-(BM+AM)=BC-AB=4-2=2,
∴③正确,
④方法一:如图,
由①得,CN=CF-FN=2-AM,AE=$\frac{1}{2}$AD=2,AM=FN
∵tanα=$\frac{AM}{AE}$,
∴AM=AEtanα
∵cosα=$\frac{AE}{ME}$=$\frac{AE}{\sqrt{A{E}^{2}+A{M}^{2}}}$,
∴cos2α=$\frac{A{E}^{2}}{A{E}^{2}+A{M}^{2}}$,
∴$\frac{1}{co{s}^{2}α}$=1+$\frac{A{M}^{2}}{A{E}^{2}}$=1+($\frac{AM}{AE}$)2=1+tan2α,
∴$\frac{2}{co{s}^{2}α}$=2(1+tan2α)
∴S△EMN=S四边形ABNE-S△AME-S△MBN
=$\frac{1}{2}$(AE+BN)×AB-$\frac{1}{2}$AE×AM-$\frac{1}{2}$BN×BM
=$\frac{1}{2}$(AE+BC-CN)×2-$\frac{1}{2}$AE×AM-$\frac{1}{2}$(BC-CN)×CN
=$\frac{1}{2}$(AE+BC-CF+FN)×2-$\frac{1}{2}$AE×AM-$\frac{1}{2}$(BC-2+AM)(2-AM)
=AE+BC-CF+AM-$\frac{1}{2}$AE×AM-$\frac{1}{2}$(2+AM)(2-AM)
=AE+AM-$\frac{1}{2}$AE×AM+$\frac{1}{2}$AM2
=AE+AEtanα-$\frac{1}{2}$AE2tanα+$\frac{1}{2}$AE2tan2α
=2+2tanα-2tanα+2tan2α
=2(1+tan2α)
=$\frac{2}{co{s}^{2}α}$.
方法二,∵E是AD的中点,
∴AE=$\frac{1}{2}$AD=2,
在Rt△AEM,cosα=$\frac{AE}{EM}$,
∴EM=$\frac{AE}{cosα}$=$\frac{2}{cosα}$,
由(1)知,Rt△AME≌Rt△FNE,
∴EM=EN,∠AEM=∠FEN,
∵∠AEF=90°,
∴∠MEN=90°,
∴△MEN是等腰直角三角形,
∴S△MEN=$\frac{1}{2}$EM2=$\frac{2}{co{s}^{2}α}$.
∴④正确.
故选C.
点评 此题是全等三角形的性质和判定题,主要考查了全等三角形的性质和判定,图形面积的计算锐角三角函数,解本题的关键是Rt△AME≌Rt△FNE,难点是计算S△EMN.

| A. | x2+2x=3x2 | B. | x6÷x2=x3 | C. | x2•(2x3)=2x5 | D. | (3x2)2=6x2 |
| A. | $\frac{1}{a+b}$ | B. | $\frac{2}{a+b}$ | C. | $\frac{a+b}{ab}$ | D. | a+b |
 如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$-2 | D. | 4-2$\sqrt{3}$ |
| A. | a3-a2=a | B. | a2•a3=a6 | C. | (3a)3=9a3 | D. | (a2)2=a4 |
| A. | x2+x2=x4 | B. | 2x3-x3=x3 | C. | x2•x3=x6 | D. | (x2)3=x5 |
 如图,D、E是△ABC边AB、AC上的两点,AD:DB=2:1,DE∥BC,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示).
如图,D、E是△ABC边AB、AC上的两点,AD:DB=2:1,DE∥BC,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示).