题目内容
已知:如图 28.1-19,△ABC内接于⊙O,点D在OC的延长线上,sinB=
28.1-19,△ABC内接于⊙O,点D在OC的延长线上,sinB= ,∠CAD=30°.
,∠CAD=30°.
(1)求证:AD是⊙O的切线;
(2)若OD⊥AB ,BC=5,求AD的长.
,BC=5,求AD的长.
(1)证明:如图,连接OA.

∵sinB= ,∴∠B=30°.∴∠AOD=60°.
,∴∠B=30°.∴∠AOD=60°.
∵OA=OC,∴△ACO是等边三角形.
∴∠OAD=60°.
∴∠OAD=90°.∴AD是⊙O的切线.
(2)解:∵OD⊥AB ∴ OC垂直平分AB.
∴ AC=BC=5.∴OA=5.
在Rt△OAD中,由 正切定义,有tan∠AOD=
正切定义,有tan∠AOD=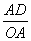 .
.
∴ AD=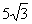 .
.

练习册系列答案
相关题目
某公司80名职工的月工资如下:
| 月工资(元) | 18 000 | 12 000 | 8 000 | 6 000 | 4 000 |
| 人数 | 1 | 2 | 3 | 4 | 10 |
| 月工资(元) | 2 500 | 2 000 | 1 500 | 1 200 | |
| 人数 | 20 | 22 | 12 | 6 |
则该公司职工月工资数据中的众数是 .

 B.
B. C.
C. D.
D.

 = .
= . 从与B地水平距离相距(BD=21米)21米远的建筑物CD的顶端C点测得A点的仰角为45°,B点的俯角为30°,现在离B点25米远的地方有一受保护的文物,则该文物是否在危险区内?试说明理由.(
从与B地水平距离相距(BD=21米)21米远的建筑物CD的顶端C点测得A点的仰角为45°,B点的俯角为30°,现在离B点25米远的地方有一受保护的文物,则该文物是否在危险区内?试说明理由.(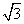 ≈1.732,精确到0.01米)
≈1.732,精确到0.01米)
 1)cm的正方形纸片中剪去一个边长为(a-1)cm
1)cm的正方形纸片中剪去一个边长为(a-1)cm
