题目内容
13. 如图,E,F分别是AB,CD上的一点,∠2=∠D,∠1与∠C互余,EC⊥AF,求证:AB∥CD.
如图,E,F分别是AB,CD上的一点,∠2=∠D,∠1与∠C互余,EC⊥AF,求证:AB∥CD.
分析 因为EC⊥AF,所以∠2+∠C=90°,又因为∠1+∠C=90°,根据同角的余角相等可得∠1=∠2,已知∠2=∠D,则有∠1=∠D,故AB∥CD.此题方法不唯一,正确就行.
解答 证明:∵EC⊥AF,
∴∠2+∠C=90°,
又∵∠1与∠C互余,
∴∠1+∠C=90°,
∴∠1=∠2,
∵∠2=∠D,
∴∠1=∠D,
∴AB∥CD.
点评 考查了平行线的判定,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.注意同角的余角相等及等量代换的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°.在OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线PR恰好与OB平行,则∠QPB的度数是( )
如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°.在OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线PR恰好与OB平行,则∠QPB的度数是( )
 如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°.在OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线PR恰好与OB平行,则∠QPB的度数是( )
如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°.在OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线PR恰好与OB平行,则∠QPB的度数是( )| A. | 60° | B. | 80° | C. | 100° | D. | 120° |
3.计算:$\sqrt{32}$-$\sqrt{8}$的结果是( )
| A. | $\sqrt{30}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2.8 |
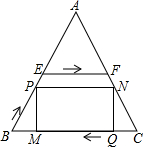 如图,在等边三角形ABC中,BC=180,E,F分别是AB,AC的中点,点P从点B出发,沿折线段BE-EF以每秒6个单位长的速度向点F匀速运动,点Q从点C出发沿线段CB方向以每秒3个单位长的速度向点B匀速运动,点P,Q同时出发,当点P与点F重合时点P停止运动,点Q也随之停止,设点P的运动时间为t秒.
如图,在等边三角形ABC中,BC=180,E,F分别是AB,AC的中点,点P从点B出发,沿折线段BE-EF以每秒6个单位长的速度向点F匀速运动,点Q从点C出发沿线段CB方向以每秒3个单位长的速度向点B匀速运动,点P,Q同时出发,当点P与点F重合时点P停止运动,点Q也随之停止,设点P的运动时间为t秒.