题目内容
17.解不等式组:$\left\{\begin{array}{l}3x-1>2({x-1})\\ \frac{x-2}{2}≤1\end{array}\right.$,并在数轴上表示出其解集.分析 分别解每个不等式,两个不等式的解集的公共部分就是所求.
解答 解:$\left\{\begin{array}{l}{3x-1>2(x-1)…①}\\{\frac{x-2}{2}≤1…②}\end{array}\right.$,
解①得:x>-1;
解②得:x≤4.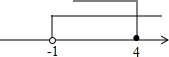 ,
,
不等式组的解集是:-1<x≤4.
点评 本题考查了不等式组的解法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
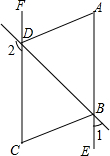 如图,已知∠1+∠2=180°,∠A=∠C,试说明AD∥BC的理由.
如图,已知∠1+∠2=180°,∠A=∠C,试说明AD∥BC的理由.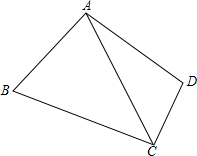 如图所示四边形ABCD,AB=AD,∠BAD=∠BCD=90°,SABCD=24cm2,求AC的长.
如图所示四边形ABCD,AB=AD,∠BAD=∠BCD=90°,SABCD=24cm2,求AC的长.