题目内容
7.化简:$\frac{{a}^{\frac{4}{3}}-8{a}^{\frac{1}{3}}b}{{a}^{\frac{2}{3}}+2\root{3}{ab}+4{b}^{\frac{2}{3}}}$÷(${a}^{-\frac{2}{3}}$-$\frac{2\root{3}{b}}{a}$)•$\frac{\sqrt{a•\root{3}{{a}^{2}}}}{\root{5}{\sqrt{a}•\root{3}{a}}}$.分析 可设x=$\root{3}{a}$,y=$\root{3}{b}$,将原式变形为$\frac{{x}^{4}-8x{y}^{3}}{{x}^{2}+2xy+4{b}^{2}}$÷$\frac{x-2y}{{x}^{3}}$•$\frac{\sqrt{{x}^{5}}}{\root{5}{{x}^{3}}•x}$,再因式分解,约分计算即可求解.
解答 解:设x=$\root{3}{a}$,y=$\root{3}{b}$,
$\frac{{a}^{\frac{4}{3}}-8{a}^{\frac{1}{3}}b}{{a}^{\frac{2}{3}}+2\root{3}{ab}+4{b}^{\frac{2}{3}}}$÷(${a}^{-\frac{2}{3}}$-$\frac{2\root{3}{b}}{a}$)•$\frac{\sqrt{a•\root{3}{{a}^{2}}}}{\root{5}{\sqrt{a}•\root{3}{a}}}$
=$\frac{{x}^{4}-8x{y}^{3}}{{x}^{2}+2xy+4{y}^{2}}$÷$\frac{x-2y}{{x}^{3}}$•$\frac{\sqrt{{x}^{5}}}{\root{5}{\sqrt{{x}^{3}}•x}}$
=$\frac{x(x-2y)({x}^{2}+2xy+4{y}^{2})}{{x}^{2}+2xy+4{y}^{2}}$•$\frac{{x}^{3}}{x-2y}$•$\frac{{x}^{2}\sqrt{x}}{\sqrt{x}}$
=x6
=a2.
点评 考查了分数指数幂,本题通过换元,将原式变形为$\frac{{x}^{4}-8x{y}^{3}}{{x}^{2}+2xy+4{b}^{2}}$÷$\frac{x-2y}{{x}^{3}}$•$\frac{\sqrt{{x}^{5}}}{\root{5}{{x}^{3}}•x}$求解.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{ab}{a+b}$ | B. | $\frac{1}{a+b}$ | C. | $\frac{1}{a}$+$\frac{1}{b}$ | D. | $\frac{1}{ab}$ |
| A. | 1+$\sqrt{23}$ | B. | 4+$\sqrt{26}$ | C. | 4+$\sqrt{15}$ | D. | 4+$\sqrt{3}$ |
| 行驶时间t(h) | 0 | 1 | 2 | 3 | 4 | … |
| 油箱中的剩余油量Q(1) | 54 | 46.5 | 39 | 31.5 | 24 | … |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)随着行驶的时间的不断增加,油箱中的剩余油量的变化趋势是怎样的?
(3)请直接写出Q与t的关系式,并求出这辆汽车在连续行驶6h后,油箱中的剩余油量;
(4)这辆车在中途不加油的情况下,最多能连续行驶的时间是多少?
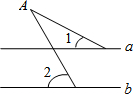 如图,已知直线a∥b,∠1=28°,∠2=52°,那么∠A的度数是24°.
如图,已知直线a∥b,∠1=28°,∠2=52°,那么∠A的度数是24°.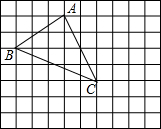 如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1),
如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1),