题目内容
13. 如图,在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥CD点P,求∠FPC的度数.
如图,在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥CD点P,求∠FPC的度数.
分析 首先延长PF交AB的延长线于点G.根据已知可得∠B,∠BEF,∠BFE的度数,再根据余角的性质可得到∠EPF的度数,从而不难求得∠FPC的度数.
解答 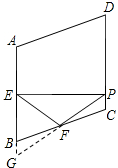 解:延长PF交AB的延长线于点G.
解:延长PF交AB的延长线于点G.
在△BGF与△CPF中,
$\left\{\begin{array}{l}{∠GBF=∠PCF}\\{BF=CF}\\{∠BFG=∠CFP}\end{array}\right.$,
∴△BGF≌△CPF(ASA),
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEP=90°,
∴EF=$\frac{1}{2}$PG,
∵PF=$\frac{1}{2}$PG,
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPC=90°,
∴∠BEP-∠FEP=∠EPC-∠EPF,即∠BEF=∠FPC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=$\frac{1}{2}$(180°-70°)=55°,
∴∠FPC=55°.
点评 此题主要考查了菱形的性质以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
1.对某班的男生进行单杠引体向上的测试,以做7次为标准,超过的次数用正数表示,不足的次数用负数表示,其中一组的8名男生的成绩如下表,这组男生的达标率(完成7个或7个以上均为达标)为多少?
| 2 | -1 | 0 | 0 | 2 | -3 | -1 | 1 |
9.西北某地区为改造沙漠,决定从2012年起进行“治沙种草”,把沙漠地变为草地,并出台了一项激励措施:在“治沙种草”的过程中,每一年新增草地面积达到10亩的农户,当年都可得到生活补贴费1500元,且每超出一亩,政府还给予每亩a元的奖励.另外,经治沙种草后的土地从下一年起,平均每亩每年可有b元的种草收入.下表是某农户在头两年通过“治沙种草”每年获得的总收入情况:
(注:年总收入=生活补贴费+政府奖励费+种草收入)
(1)试根据提供的资料确定a、b的值;
(2)观察数据,2013的新增草地的亩数在2012年新增草地的亩数上增加了一个百分数,若从2013年起,该农户每年新增草地的亩数均能比前一年按这个百分数增长,那么2015年该农户通过“治沙种草”获得的年总收入将达到多少元?
(注:年总收入=生活补贴费+政府奖励费+种草收入)
| 年份 | 新增草地的亩数 | 年总收入 |
| 2012年 | 20亩 | 2600元 |
| 2013年 | 26亩 | 5060元 |
(2)观察数据,2013的新增草地的亩数在2012年新增草地的亩数上增加了一个百分数,若从2013年起,该农户每年新增草地的亩数均能比前一年按这个百分数增长,那么2015年该农户通过“治沙种草”获得的年总收入将达到多少元?
