题目内容
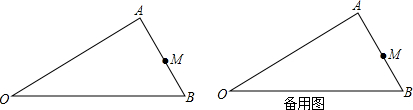
12.已知:如图,点M是锐角△AOB的AB边上任意一点.(1)请在OA边上求作一点P,在OB边上求作一点Q,使得△PMQ的周长最小;如果OM=2,∠AOB=30°,求此时△PMQ的周长.
作法:作M关于OA的对称点M′,作M关于OB的对称点M″,连接M′M″交OA于P,交OB于Q,则线段M′M″的长度=△PMQ的周长最小值;
(2)当点M在AB边上运动时,△PMQ的周长会发生变化吗?如果会发生变化,请研究△PMQ的周长何时会取到最小值.
分析 (1)作M关于OA的对称点M′,作M关于OB的对称点M″,连接M′M″交OA于P,交OB于Q,于是得到线段M′M″的长度=△PMQ的周长最小值,连接OM′,OM″,OM,根据轴对称的性质得到OM=OM′=OM″,∠M′OA=∠MOA,∠MOB=∠M″OB,推出△M′OM″是等边三角形,即可得到结论;
(2)△PMQ的周长会发生变化,由(1)知,△PMQ的周长=M′M″,当△PMQ的周长取到最小值时,M′M″取到最小值,由于M′M″=OM,于是得到OM⊥AB时,OM取到最小值,即可得到结论.
解答 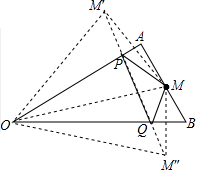 解:(1)作法:作M关于OA的对称点M′,作M关于OB的对称点M″,连接M′M″交OA于P,交OB于Q,则线段M′M″的长度=△PMQ的周长最小值,
解:(1)作法:作M关于OA的对称点M′,作M关于OB的对称点M″,连接M′M″交OA于P,交OB于Q,则线段M′M″的长度=△PMQ的周长最小值,
连接OM′,OM″,OM,
∴OM=OM′=OM″,∠M′OA=∠MOA,∠MOB=∠M″OB,
∵∠AOB=30°,
∴∠M′OM″=60°,
∴△M′OM″是等边三角形,
∴M′M″=OM=2,
∴此时△PMQ的周长=2;
故答案为:作M关于OA的对称点M′,作M关于OB的对称点M″,连接M′M″交OA于P,交OB于Q,则线段M′M″的长度=△PMQ的周长最小值,
(2)△PMQ的周长会发生变化,
由(1)知,△PMQ的周长=M′M″,
当△PMQ的周长取到最小值时,
M′M″取到最小值,
∵M′M″=OM,
∴OM取到最小值,
∴OM⊥AB时,OM取到最小值,
即OM⊥AB时,△PMQ的周长取到最小值.
点评 此题主要考查轴对称--最短路线问题,线段的性质,熟知两点之间线段最短是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2.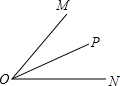 已知,如图,OP平分∠MON,则下列式子中错误的是( )
已知,如图,OP平分∠MON,则下列式子中错误的是( )
 已知,如图,OP平分∠MON,则下列式子中错误的是( )
已知,如图,OP平分∠MON,则下列式子中错误的是( )| A. | ∠MOP=∠NOP | B. | ∠MOP=$\frac{1}{2}$∠MON | C. | ∠MON=2∠NOP | D. | ∠MOP+∠NOP>∠MON |
3.在-13,0,2,11这四个数中,最小的数是( )
| A. | -13 | B. | 0 | C. | 2 | D. | 11 |
 已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P,在OB边上求作一点Q,使得MP+PQ最小.若OM=2,OM平分∠AOB,并且∠AOB=20°,求这个最小值.
已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P,在OB边上求作一点Q,使得MP+PQ最小.若OM=2,OM平分∠AOB,并且∠AOB=20°,求这个最小值.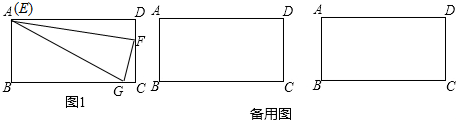
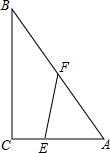 如图,在Rt△ABC中,∠C=90,AC=3,BC=4,点E在直角边AC上(点E与A、C两点均不重合),点F在斜边AB上(点F与A、B两点均不重合).
如图,在Rt△ABC中,∠C=90,AC=3,BC=4,点E在直角边AC上(点E与A、C两点均不重合),点F在斜边AB上(点F与A、B两点均不重合).