题目内容
5.如图1,A、B两地相距90km,甲、乙二人同时从A地出发向B地行进,甲以高于乙10km/h的骑车速度前行,行驶一段时间后因某些原因又往回骑行(在往返过程中速度不变),与乙汇合后,二人继续以各自的速度向B地行进,设两人骑行的时间为t,与A地的距离为s,s与t之间的函数图象如图2所示.(1)甲、乙两人骑行的速度;
(2)若乙从A地出发$\frac{3}{5}$小时后,丙以35km/h的速度由B地向A骑行,则丙经过1或$\frac{3}{2}$小时后,与乙相距15km.
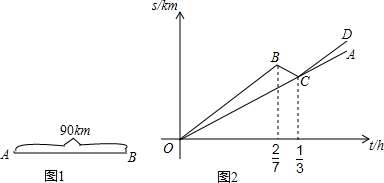
分析 (1)设甲骑行的速度为xkm/h,则乙的速度是(x-10)km/h,根据图中的数据列出方程求解即可;
(2)设丙经过m小时后,与乙相距15km,分当两人第一次相距15km时和两人第二次相距15km时,分别列出方程求解即可.
解答 解:(1)设甲骑行的速度为xkm/h,则乙的速度是(x-10)km/h,根据题意得:
[$\frac{2}{7}$-($\frac{1}{3}$-$\frac{2}{7}$)]x=$\frac{1}{3}$(x-10),
解得;x=35,
则x-10=35-10=25(km/h),
答:甲骑行的速度为35km/h,乙的速度是25km/h;
(2)设丙经过m小时后,与乙相距15km,当两人第一次相距15km时,根据题意得:
$\frac{3}{5}$×25+25x+35x=90-15,
解得:m=1,
当两人第二次相距15km时,根据题意得:
$\frac{3}{5}$×25+25x+35x=90+15,
解得:m=$\frac{3}{2}$,
答:丙经过1或$\frac{3}{2}$小时后,与乙相距15km;
故答案为:1或$\frac{3}{2}$.
点评 此题考查了一元一次方程的应用,解题关键是找出题目中的等量关系,列出方程,本题要注意分两种情况列方程,不要漏解.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
20. 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}-1$ |
10.若菱形的两条对角线的长分别为6,8.则此菱形的周长是( )
| A. | 14 | B. | 20 | C. | 28 | D. | 40 |
14.已知反比例函数的图象经过点(-2,4),当x=4时,所对应的函数值y等于( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
15.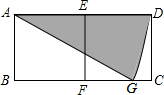 如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
 如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
 如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的三角形,请你帮助小华作出来.
如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的三角形,请你帮助小华作出来.