题目内容
6. 如图,直线y=-$\frac{3}{4}x+3$与y轴、x轴分别交于点A、B,x轴上有点P,使得△ABP为等腰三角形,则P的坐标为($\frac{7}{8}$,0)或(-1,0)或(9,0)或(-4,0).
如图,直线y=-$\frac{3}{4}x+3$与y轴、x轴分别交于点A、B,x轴上有点P,使得△ABP为等腰三角形,则P的坐标为($\frac{7}{8}$,0)或(-1,0)或(9,0)或(-4,0).
分析 求出A、B的坐标,求出OA、OB、AB,分为三种情况:画出图形,根据等腰三角形的判定求出即可.
解答 解:直线y=-$\frac{3}{4}x+3$,
当x=0时,y=3,
当y=0时,x=4,
即A(0,3),B(4,0),
OA=3,OB=4,
由勾股定理得:AB=5,
分为三种情况:①如图1,作AB的垂直平分线EP,垂足为E,交x轴于P,此时AP=BP,
则BE=AE=$\frac{5}{2}$,
∵∠AOB=∠PEB=90°,∠ABO=∠EBP,
∴△PEB∽△AOB,
∴$\frac{BP}{AB}$=$\frac{BE}{OB}$,
∴$\frac{BP}{5}$=$\frac{\frac{5}{2}}{4}$,
∴BP=$\frac{25}{8}$,
∴OP=4-BP=$\frac{7}{8}$,
此时P的坐标为($\frac{7}{8}$,0);
②如图2,以B为圆心以AB为半径画弧,交x轴交于两点P2,P3,
此时AB=BP,
点P的坐标为(-1,0)和(9,0);
③如图3,以A为圆心以AB为半径画弧,交x轴交于点P4,
此时AB=AP=5,
点P的坐标为(-4,0).
故答案为:($\frac{7}{8}$,0)或(-1,0)或(9,0)或(-4,0).
点评 本题考查了等腰三角形的判定,坐标与图形性质的应用,能求出符合的所有情况是解此题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
9.射线OC,OD分别是∠AOB的三等分线,且OC,OD分别垂直于∠AOB的两边,那么∠AOB为( )
| A. | 90° | B. | 112.5° | C. | 135° | D. | 120° |
14. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
①△BDE∽△DPE;②$\frac{FP}{PH}$=$\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.
其中正确的是( )
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②$\frac{FP}{PH}$=$\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.
其中正确的是( )
| A. | ①②③④ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
16.计算2.7×10-8-2.6×10-8,结果用科学记数法表示为( )
| A. | 0.1×10-8 | B. | 0.1×10-7 | C. | 1×10-8 | D. | 1×10-9 |
 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C. 汽车正在行驶可车轮突然陷入无盖井,骑车人正在快速前行却因突然出现在面前的凸起井盖被摔伤,夜间出门时被一个没有井盖的窖井吞噬…全国各地因为井盖缺失而造成事故的情形不绝于耳,井盖吞人事件更是频频发生,为了保障市民的人身安全,合肥市政部门开始更换质量更好的井盖(如图所示).小明想知道井盖的半径,在⊙O上,取了三个点A、B、C,测量出AB=AC=50,BC=80,请你帮助小明求出井盖的半径,写出计算过程.
汽车正在行驶可车轮突然陷入无盖井,骑车人正在快速前行却因突然出现在面前的凸起井盖被摔伤,夜间出门时被一个没有井盖的窖井吞噬…全国各地因为井盖缺失而造成事故的情形不绝于耳,井盖吞人事件更是频频发生,为了保障市民的人身安全,合肥市政部门开始更换质量更好的井盖(如图所示).小明想知道井盖的半径,在⊙O上,取了三个点A、B、C,测量出AB=AC=50,BC=80,请你帮助小明求出井盖的半径,写出计算过程.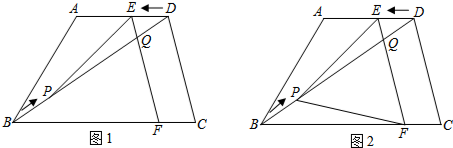
 苹果熟了,一个苹果从树上被抛下.如图所示,从A处落到了B处.(网格单位长度为1)
苹果熟了,一个苹果从树上被抛下.如图所示,从A处落到了B处.(网格单位长度为1)