题目内容
5.二次函数y=ax2+bx+c(a≠0)与x轴的两个交点之间的距离可以用a,b,c的代数表示为$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$.请利用以上结论,求二次函数y=x2+(k+4)x+k的图象与x轴两个交点间的最短距离为2$\sqrt{3}$.分析 根据公式求出两个交点之间的距离d,再利用二次函数的性质即可解决.
解答 解:设两个交点之间的距离为d,则d=$\sqrt{(k+4)^{2}-4k}$=$\sqrt{(k+2)^{2}+12}$,
当x=12时,d的最小值=$\sqrt{12}$=2$\sqrt{3}$,
故答案为2$\sqrt{3}$.
点评 本题考查二次函数与x轴的交点问题、最值问题,学会利用二次函数的性质解决最值问题,关键是熟练运用配方法,属于中考常考题型.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
16.定义:a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数,如2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数是$\frac{1}{1-(-1)}$=$\frac{1}{2}$.已知a1=-$\frac{1}{2}$,a2是a1的差倒数,a3是a2的差倒数,a4是 a3的差倒数,…,以此类推,则a2016为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | 1 |
12.下列关于平角和周角的说法正确的是( )
| A. | 平角是一条线段 | B. | 周角是一条射线 | ||
| C. | 两个锐角的和不一定小于平角 | D. | 反向延长射线OA,就形成一个平角 |
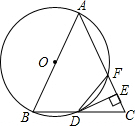 如图,以等腰△ABC的一腰AB为直径的圆交底边BC于点D,交另一腰AC于点F,连接DF,过点D作DE⊥AC于点E.
如图,以等腰△ABC的一腰AB为直径的圆交底边BC于点D,交另一腰AC于点F,连接DF,过点D作DE⊥AC于点E. 如图,在平面直角坐标系中,点A的坐标为(0,2),点p的坐标为(m,0)且m>0,一开口向上的抛物线以P为顶点,且经过点A.
如图,在平面直角坐标系中,点A的坐标为(0,2),点p的坐标为(m,0)且m>0,一开口向上的抛物线以P为顶点,且经过点A.