题目内容
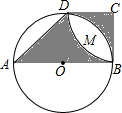 如图,已知AB是⊙O的直径,点D在⊙O上,四边形ABCD是梯形,AB⊥BC,DC⊥BC,AB=2DC,
如图,已知AB是⊙O的直径,点D在⊙O上,四边形ABCD是梯形,AB⊥BC,DC⊥BC,AB=2DC, |
| DMB |
| 22 |
| 7 |
考点:扇形面积的计算
专题:
分析:连结BD,设⊙O的半径为r,则OB=BC=CD=r.先求出梯形ABCD内部空白部分的面积=2(S扇形DCB-S△DCB)=2×(
-
r2)=(
π-1)r2,那么图中阴影部分的面积=S梯形ABCD-S空白=
(r+2r)•r-(
π-1)r2=(
-
π)r2,再求出⊙O的面积=πr2,进而得到图中阴影部分的面积与⊙O的面积之比.
| 90π•r2 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
解答:解: 如图,连结BD,设⊙O的半径为r,则OB=BC=CD=r.
如图,连结BD,设⊙O的半径为r,则OB=BC=CD=r.
∵梯形ABCD内部空白部分的面积=2(S扇形DCB-S△DCB)=2×(
-
r2)=(
π-1)r2,
∴图中阴影部分的面积=S梯形ABCD-S空白=
(r+2r)•r-(
π-1)r2=(
-
π)r2,
又∵⊙O的面积=πr2,π取
,
∴图中阴影部分的面积与⊙O的面积之比为
=
.
故答案为
.
 如图,连结BD,设⊙O的半径为r,则OB=BC=CD=r.
如图,连结BD,设⊙O的半径为r,则OB=BC=CD=r.∵梯形ABCD内部空白部分的面积=2(S扇形DCB-S△DCB)=2×(
| 90π•r2 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
∴图中阴影部分的面积=S梯形ABCD-S空白=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
又∵⊙O的面积=πr2,π取
| 22 |
| 7 |
∴图中阴影部分的面积与⊙O的面积之比为
(
| ||||
| πr2 |
| 13 |
| 44 |
故答案为
| 13 |
| 44 |
点评:本题考查了扇形面积的计算,准确作出辅助线,求出梯形ABCD内部空白部分的面积是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
在下列方程中,一元二次方程的个数是( )
①3x2+7=0;②ax2+bx+c=0;③x2+2x-3;④3x2-
=0.
①3x2+7=0;②ax2+bx+c=0;③x2+2x-3;④3x2-
| 5 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
△ABC中,∠C=90°,AB=10,cosB=
,△ABC的面积是( )
| 3 |
| 5 |
| A、48 | B、40 | C、30 | D、24 |
 如图,已知∠1=∠2,∠B=∠C,AF=AE,求证:CD=BD.
如图,已知∠1=∠2,∠B=∠C,AF=AE,求证:CD=BD.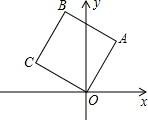 如图,正方形OABC的边长为4,若OA与x轴的正方向成60°,求A,C的坐标.
如图,正方形OABC的边长为4,若OA与x轴的正方向成60°,求A,C的坐标.