题目内容
△ABC中,∠C=90°,AB=10,cosB=
,△ABC的面积是( )
| 3 |
| 5 |
| A、48 | B、40 | C、30 | D、24 |
考点:解直角三角形
专题:
分析:通过解该直角三角形可以求得AC、BC的长度,然后利用三角形的面积公式进行解答.
解答: 解:如图,∵△ABC中,∠C=90°,AB=10,cosB=
解:如图,∵△ABC中,∠C=90°,AB=10,cosB=
,
∴
=
=
,则BC=6.
又由勾股定理得 AC=
=
=8,
∴△ABC的面积是:
AC•BC=
×8×6=24.
故选:D.
 解:如图,∵△ABC中,∠C=90°,AB=10,cosB=
解:如图,∵△ABC中,∠C=90°,AB=10,cosB=| 3 |
| 5 |
∴
| BC |
| AB |
| BC |
| 10 |
| 3 |
| 5 |
又由勾股定理得 AC=
| AB2-BC2 |
| 102-62 |
∴△ABC的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查了解直角三角形.解这个直角三角形,可求出相关边的长度.

练习册系列答案
相关题目
下列图形中不是中心对称的图形是( )
| A、矩形 | B、菱形 |
| C、正方形 | D、等腰梯形 |
在下列给出的条件中,不能判定两个三角形全等的是( )
| A、两边一角分别相等 |
| B、两角一边分别相等 |
| C、直角边和一锐角分别相等 |
| D、三边分别相等 |
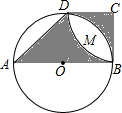 如图,已知AB是⊙O的直径,点D在⊙O上,四边形ABCD是梯形,AB⊥BC,DC⊥BC,AB=2DC,
如图,已知AB是⊙O的直径,点D在⊙O上,四边形ABCD是梯形,AB⊥BC,DC⊥BC,AB=2DC,
 用“>”或“<”号填空:
用“>”或“<”号填空: 如图,已知矩形ABCD,AB=2,AD=4,点P在BC上移动,△ABP和△PCD能相似吗?若能,求出点P的位置;若不能,请说明理由.
如图,已知矩形ABCD,AB=2,AD=4,点P在BC上移动,△ABP和△PCD能相似吗?若能,求出点P的位置;若不能,请说明理由.