题目内容
二次函数y=x2+x-6的图象与x轴两个交点的坐标分别为( )
| A、(2,0),(-3,0) |
| B、(-2,0),(3,0) |
| C、(2,0),(3,0) |
| D、(-2,0),(-3,0) |
考点:抛物线与x轴的交点
专题:
分析:由于函数图象与x轴的交点纵坐标为0,于是可令y=0,得到方程,解答即可.
解答:解:当y=0时,x2+x-6=0,
即(x-2)(x+3)=0,
解得x1=2,x2=-3,
则抛物线与x轴的交点为(2,0),(-3,0).
故选A.
即(x-2)(x+3)=0,
解得x1=2,x2=-3,
则抛物线与x轴的交点为(2,0),(-3,0).
故选A.
点评:本题考查了抛物线与x轴的交点,令y=0,得到一元二次方程,方程的解即为与x轴交点的横坐标.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 实数a,b在数轴上对应的点的位置如图,则必有( )
实数a,b在数轴上对应的点的位置如图,则必有( )A、
| ||
| B、ab>0 | ||
| C、a-|b|>0 | ||
| D、a+b>0 |
下列四个算式中,正确的是( )
| A、(-5)+(+3)=-8 | ||
| B、-3+|-3|=0 | ||
C、(-1)÷5×
| ||
| D、-(-2)3=6 |
直线y=kx+b与y=2x平行,和y轴交于点(0,3),则该函数关系式是( )
| A、y=2x-3 |
| B、y=3x+2 |
| C、y=2x+3 |
| D、y=3x-2 |
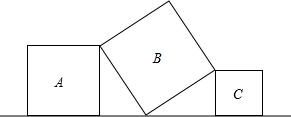 如图,将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,C的边长为3,则B的边长为
如图,将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,C的边长为3,则B的边长为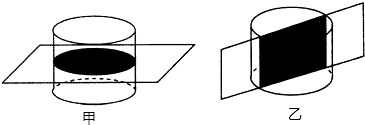 一个平面去截一个圆柱,图甲中截面的形状是
一个平面去截一个圆柱,图甲中截面的形状是 在正方形ABCD中,E是AD的中点,求tan∠ABE的值.
在正方形ABCD中,E是AD的中点,求tan∠ABE的值.