��Ŀ����
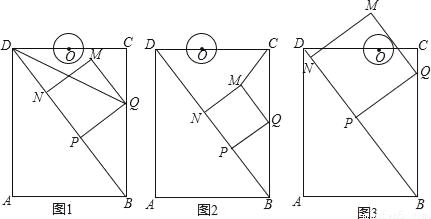
��ͼ���ھ���ABCD�У�AB=6cm��AD=8cm����P�ӵ�B�������ضԽ���BD���D�����˶����ٶ�Ϊ4cm/s������P��PQ��BD��BC�ڵ�Q����PQΪһ����������PQMN��ʹ�õ�N��������PD�ϣ���O�ӵ�D��������DC���C�����˶����ٶ�Ϊ3cm/s����OΪԲ�ģ�0.8cmΪ�뾶��ԲO����P���Oͬʱ�����������ǵ��˶�ʱ��Ϊt����λ��s����0��t��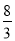 ��
��
��1����ͼ1������DQ����DQƽ�֡�BDCʱ��t��ֵΪ�� ��
��2����ͼ2������CM������CMQ����CQΪ�ĵ��������Σ���t��ֵ��
��3�������������̽����������������⣺
��֤�������˶������У���Oʼ����QM����ֱ�ߵ���ࣻ
����ͼ3�����˶������У���QM��ԲO����ʱ����t��ֵ�����жϴ�ʱPM��ԲO�Ƿ�Ҳ���У�˵�����ɣ�
��ϰ��ϵ�д�
 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д�
�����Ŀ


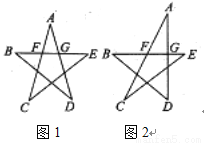

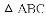
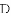
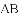
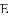
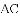
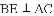
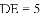
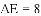
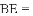
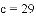
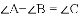
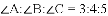
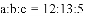
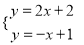 �Ľ�Ϊ����ĵ㣨x��y���ڵ�_____���ޣ�
�Ľ�Ϊ����ĵ㣨x��y���ڵ�_____���ޣ�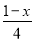 =��1ȥ��ĸ��ȷ���ǣ� ��
=��1ȥ��ĸ��ȷ���ǣ� ��