题目内容
8.若抛物线y=kx2-2x-1顶点在x轴上,则k值是-1.分析 抛物线y=kx2-2x-1顶点在x轴上,则对应的判别式△=0,据此即可求解.
解答 解:根据题意得:△=4+4k=0,且k≠0.
解得:k=-1.
故答案是:-1.
点评 本题考查了二次函数的性质,判别式△>0,则函数与x轴有两个交点;当△=0时,抛物线与x轴只有一个公共点,即顶点在x轴上;当△<0时,抛物线与x轴没有交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列说法中正确的是( )
| A. | 单项式-$\frac{2}{3}$a2b的系数为-2 | B. | 多项式-3a2b+7a2b2+1的次数是3 | ||
| C. | a和0都是单项式 | D. | x2+$\frac{2}{y}$是整式 |
17.一元二次方程x2=3x的解为( )
| A. | x=0 | B. | x=3 | C. | x=0或x=3 | D. | x=0 且x=3 |
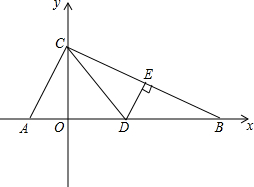 如图,在平面直角坐标系内,已知A(-4,0),B(16,0),点C在y轴正半轴上,且∠ACB=90°,D,E分别为线段AB,BC上的点,把△BDE沿直线DE翻折,使点B落在点C处.
如图,在平面直角坐标系内,已知A(-4,0),B(16,0),点C在y轴正半轴上,且∠ACB=90°,D,E分别为线段AB,BC上的点,把△BDE沿直线DE翻折,使点B落在点C处. 如图,已知二次函数y=x2+bx+4与x轴交于点B(4,0),与y轴交于点A,O为坐标原点,P是二次函数y=x2+bx+4的图象上一个动点,点P的横坐标是m,且m>4,过点P作PM⊥x轴,PM交直线AB于M.
如图,已知二次函数y=x2+bx+4与x轴交于点B(4,0),与y轴交于点A,O为坐标原点,P是二次函数y=x2+bx+4的图象上一个动点,点P的横坐标是m,且m>4,过点P作PM⊥x轴,PM交直线AB于M.