题目内容
5.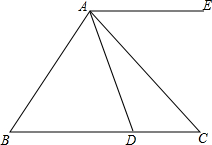 如图,已知在△ABC中,∠ABC-∠ACB=20°,∠ACB的度数是∠BAC度数的$\frac{1}{2}$.
如图,已知在△ABC中,∠ABC-∠ACB=20°,∠ACB的度数是∠BAC度数的$\frac{1}{2}$.(1)求∠ABC的度数;
(2)如果AD平分∠BAC,那么△ACD是什么三角形?
分析 (1)先设∠ACB=x,然后根据题意用含有x的式子表示∠ABC和∠BAC,然后根据三角形内角和定理即可求出∠ABC的度数;
(2)由AD平分∠BAC,可得∠DAC=$\frac{1}{2}$∠BAC=40°,然后根据三角形内角和定理可求∠ADC的度数,然后即可判断△ACD的形状.
解答 解:(1)设∠ACB=x,
∵∠ABC-∠ACB=20°,∠ACB的度数是∠BAC度数的$\frac{1}{2}$.
∴∠ABC=x+20,∠BAC=2x,
∵∠ABC+∠ACB+∠BAC=180°,
∴x+20+x+2x=180,
解得:x=40°,
∴∠ABC=x+20=60°,∠BAC=2x=80°,
∴∠ABC=60°;
(2)∵AD平分∠BAC,
∴∠DAC=$\frac{1}{2}$∠BAC=40°,
∴∠∠DAC=∠ACB,
∴AD=DC,
∵∠DAC+∠ADC+∠ACB=180°,
∴∠ADC=100°,
∴△ACD是等腰三角形.
点评 此题考查了三角形内角和定理及等腰三角形的判定,熟记三角形内角和为180°是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.用两种边长相等的正多边形地砖铺地,已有正方形的地砖,还可选择地砖形状为( )
| A. | 正五边形 | B. | 正六边形 | C. | 正八边形 | D. | 正十边形 |
 如图,点E,F是线段AB的黄金分割点,已知AB=10,求EF的长度.
如图,点E,F是线段AB的黄金分割点,已知AB=10,求EF的长度.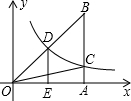 如图,已知反比例函数的图象经过直角△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为12,求这个反比例函数的解析式.
如图,已知反比例函数的图象经过直角△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为12,求这个反比例函数的解析式.