题目内容
16. 如图,在正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF相交于点M,则图中与△ABM相似的三角形有△ABM∽△FAM,△ABM∽△FBA.
如图,在正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF相交于点M,则图中与△ABM相似的三角形有△ABM∽△FAM,△ABM∽△FBA.
分析 根据正方形的性质,运用SAS证明△ABF≌△DAE,再由全等三角形的性质可得出结论.
解答 解:∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠ADE=90°.
∵CE=DF,
∴AF=DE.
在△ABF与△DAE中,
∵$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=∠ADE}\\{AF=DE}\end{array}\right.$,
∴△ABF≌△DAE(SAS).
∴AE=BF;
∴∠AFB=∠AED.
∵∠AED+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AOF=90°,即AE⊥BF.
∵∠BAF=90°,
∴∠AFB+∠ABF=90°.
∵∠ABF+∠BAM=90°,
∴∠BAM=∠AFM,
∴△ABM∽△FAM.
同理,△ABM∽△FBA.
故答案为:△ABM∽△FAM,△ABM∽△FBA.
点评 本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.

练习册系列答案
相关题目
1. 如图,点G是△ABC的重心,连接EF交AD于H,则GH:HA是( )
如图,点G是△ABC的重心,连接EF交AD于H,则GH:HA是( )
 如图,点G是△ABC的重心,连接EF交AD于H,则GH:HA是( )
如图,点G是△ABC的重心,连接EF交AD于H,则GH:HA是( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:5 |
 如图所示,已知△ABE≌△ACD,指出它们的对应边和对应角.
如图所示,已知△ABE≌△ACD,指出它们的对应边和对应角.
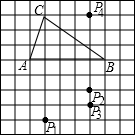 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P的个数为( )
如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P的个数为( )