题目内容
3.下表给出的是两种移动电话的计费方式:| 月使用费/元 | 主叫限定时间/min | 主叫超时费/(元/min) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
(1)设一个月内移动用移动电话主叫为x min,方式一的费用为y1元,方式二的费用为y2元,求出y1与x,y2与x之间的函数解析式,并写出自变量x的取值范围;
(2)在同一个坐标系内画出y1,y2的图象,并结合函数图象与解析式,选择最省钱的计费方式;
(3)若某用户选择的方式二,在某月中平均每分钟的话费为0.44元,求该用户这个月的主叫时间?
分析 (1)根据分段计费的费用就可以得出各个时段各种不同的付费方法就可以得出结论;
(2)画出图象,根据解析式分段探讨得出答案即可;
(3)可得主叫限定时间小于350分,根据总价÷单价=数量,列出算式求得答案即可.
解答 解:(1)由题意,得
当t≤150时,方式一收费:y1=58,方式二收费:y2=88;
当150<t<350时,方式一收费:y1=58+0.25(t-150)=0.25t+20.5;方式二收费:y2=88;
当t≥350时,方式一收费:y1=58+0.25(t-150)=0.25t+20.5;方式二收费:y2=88+0.19(t-350)=0.19t+21.5;
(2)图象如下:
t≤150时,
方式一的付费为58元,方式二的付费为88元,
∵58<88,
∴方式一计费省;
当150<t<350时,方式一的计费由58元增加到108元,方式二是88元,
当58+0.25(t-150)=88时,
解得:t=270,
∴t<270时,方式一省钱,t=270时,两种方式一样省钱,270<t<350时方式二省钱.
t≥350时,
0.25t+20.5-(0.19t+21.5)=0.06t-1>0,
∴方式二省钱.
∴综上所述,t<270时,方式一省钱,t=270时,两种方式一样省钱,t>270时方式二省钱
t<270时,方式一省钱,t=270时,两种方式一样省钱,t>270时方式二省钱.
(3)88÷0.44=200分.
答:该用户这个月的主叫时间为200分钟.
点评 此题考查一次函数的实际运用,理解题意,根据题意分段得出函数解析式是解决问题的关键.

练习册系列答案
相关题目
6.已知点(-4,y1),(2,y2)在直线y=-$\frac{1}{2}x$+b上,则y1与y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
15.在平面直角坐标系中,点P的坐标是(-3,4),下列说法正确的是( )
| A. | 点P到x轴的距离为3 | B. | 点P到x轴的距离为-3 | ||
| C. | 点P到y轴的距离为4 | D. | 点P到y轴的距离为3 |
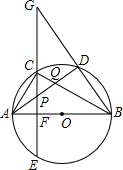 已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连结BD并延长交EC的延长线于点G,连结AD,分别交CE、BC于点P、Q.
已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连结BD并延长交EC的延长线于点G,连结AD,分别交CE、BC于点P、Q.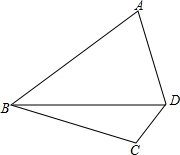 如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.
如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.