��Ŀ����
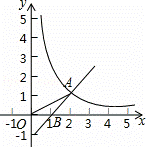
��ͼ��������A��0����6����������y=x2+bx+c��x���ཻ��B����2��0����C���㣮
��1����������ߵĺ�����ϵʽ�Ͷ���D�����ꣻ
��2������1������õ�����������ƽ��1����λ���ȣ�������ƽ��m��m��0������λ���ȵõ���������y1������������y1�Ķ���P�ڡ�ABC�ڣ���m��ȡֵ��Χ��
��3���ڣ�2���Ľ����£���������y1���Ƿ���ڵ�Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ���������п��ܳ��ֵ��������ֱ��д�����Ӧ��m��ȡֵ��Χ��

�⣺��1����A��0����6����B����2��0������y=x2+bx+c��
�ã� ��
��
��ã� ��
��
��y=x2��2x��6��
�ඥ������Ϊ��2����8����
��2������1������õ�����������ƽ��1����λ���ȣ�������ƽ��m��m��0������λ���ȵõ���������y1=��x��2+1��2��8+m��
��P��1����8+m����
��������y=x2��2x��6����C��6��0����
��ֱ��ACΪy2=x��6��
��x=1ʱ��y2=��5��
�ੁ5����8+m��0��
��ã�3��m��8��
��3����A��0����6����B����2��0����
���߶�AB���е�����Ϊ����1����3����ֱ��AB�Ľ���ʽΪy=��3x��6��
���AB���е�����AB��ֱ��ֱ�ߵĽ���ʽΪ��y=x����
��ֱ��y=x����x=1�Ľ�������Ϊ��1��������
���ʱ�ĵ�P������Ϊ��1��������
���ʱ����ƽ����8��= ����λ��
�����
��ٵ�3��m�� ʱ����������Q�㣬�������������������Σ�
ʱ����������Q�㣬�������������������Σ�
�ڵ�m= ʱ������һ����Q��������һ�����������Σ�
ʱ������һ����Q��������һ�����������Σ�
�۵� ��m��8ʱ��Q�㲻���ڣ������������������Σ�
��m��8ʱ��Q�㲻���ڣ������������������Σ�

����������ȷ���ǣ�������
| �� | A�� | ����2mn��2=4m2n2 | B�� | y2+y2=2y4 | C�� | ��a��b��2=a2��b2 | D�� | m2+m=m3 |
��ͼͼ���У�����Գ�ͼ�Σ����������ĶԳ�ͼ�ε��ǣ�������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|










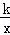 ��x��0����ͼ���ڵ�A��2��1������x�ύ�ڵ�B��
��x��0����ͼ���ڵ�A��2��1������x�ύ�ڵ�B��