��Ŀ����
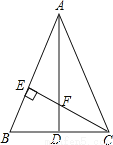
��ͼ����ABC�У�AB=AC����AD��BC��CE��AB������ֱ�ΪD��E��AD��CE�ཻ�ڵ�F������֪AE=CE.
(1)��֤����AEF�ա�CEB��
(2)��֤��AF=2CD
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ����ABC�У�AB=AC����AD��BC��CE��AB������ֱ�ΪD��E��AD��CE�ཻ�ڵ�F������֪AE=CE.
(1)��֤����AEF�ա�CEB��
(2)��֤��AF=2CD
