题目内容
5. 如图,矩形OBCD的顶点C的坐标为(2,3),则BD=$\sqrt{13}$.
如图,矩形OBCD的顶点C的坐标为(2,3),则BD=$\sqrt{13}$.
分析 连接OC,因为四边形OBCD是矩形,所以OC=BD,C的坐标为(2,3),就可求出OC的长度,那么就可求出BD的长度.
解答 解:连接OC,如图所示:

根据勾股定理得:OC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∵四边形OBCD是矩形,
∴BD=OC=$\sqrt{13}$;
故答案为:$\sqrt{13}$.
点评 本题考查了矩形的性质、坐标与图形性质、勾股定理;熟练掌握矩形的性质,运用勾股定理求出OC是解决问题的关键.

练习册系列答案
相关题目
15.下列说法,正确的是( )
| A. | 每个命题都有逆命题 | B. | 假命题的逆命题一定是假命题 | ||
| C. | 每个定理都有逆定理 | D. | 真命题是逆命题一定是真命题 |
20.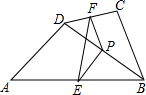 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=22°,则∠PFE的度数是( )
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=22°,则∠PFE的度数是( )
 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=22°,则∠PFE的度数是( )
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=22°,则∠PFE的度数是( )| A. | 15° | B. | 20° | C. | 22° | D. | 44° |
10.已知三角形三边长分别为3、x、10,若x为正整数,则这样的三角形个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
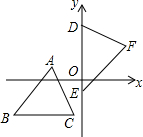 如图,直角坐标平面上,△ABC与△DEF全等,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点纵坐标都是-3,D,E两点在y轴上,则F点到y轴的距离为4.
如图,直角坐标平面上,△ABC与△DEF全等,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点纵坐标都是-3,D,E两点在y轴上,则F点到y轴的距离为4. 如图,在矩形ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,有列结论:①AF=AE ②EF=2$\sqrt{5}$③AF=EF④S△AEF=10,其中正确的结论有①②④.(填序号)
如图,在矩形ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,有列结论:①AF=AE ②EF=2$\sqrt{5}$③AF=EF④S△AEF=10,其中正确的结论有①②④.(填序号) 一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和“生”相对的面上写的汉字是活.
一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和“生”相对的面上写的汉字是活.