题目内容
20.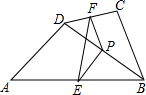 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=22°,则∠PFE的度数是( )
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=22°,则∠PFE的度数是( )| A. | 15° | B. | 20° | C. | 22° | D. | 44° |
分析 根据中位线定理和已知,证明△EPF是等腰三角形,由等腰三角形的性质即可得出答案.
解答 解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,
∴FP,PE分别是△CDB与△DAB的中位线,
∴PF=$\frac{1}{2}$BC,PE=$\frac{1}{2}$AD,
∵AD=BC,
∴PF=PE,
故△EPF是等腰三角形.
∵∠PEF=22°,
∴∠PEF=∠PFE=22°.
故选:C.
点评 本题考查了三角形中位线定理及等腰三角形的判定与性质,证明三角形是等腰三角形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,矩形OBCD的顶点C的坐标为(2,3),则BD=$\sqrt{13}$.
如图,矩形OBCD的顶点C的坐标为(2,3),则BD=$\sqrt{13}$.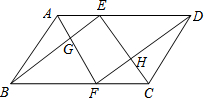 如图,在平行四边形ABCD中,点E、F分别在AD、BC边上,且AE=CF,AF与BE交于G,CE与DF交于H.求证:四边形EGFH是平行四边形.
如图,在平行四边形ABCD中,点E、F分别在AD、BC边上,且AE=CF,AF与BE交于G,CE与DF交于H.求证:四边形EGFH是平行四边形.