题目内容
2.某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)降价后,商家要使每天的销售利润最大,应将售价降价多少元?最大销售利润是多少?
分析 (1)表示出每天降价x元后售出的数量,表示出利润,解方程得到答案;
(2)运用二次函数的性质求出最大值即可.
解答 解:(1)设每件衬衣降价x元,由题意得,
(40-x)(20+2x)=1200,
解得:x1=10,x2=20,
(2)设每件衬衣降价x元,利润为y元,
y=(40-x)(20+2x)
=-2x2+60x+800,
(2)∵a=-2<0,函数有最大值
当x=-$\frac{60}{2×(-2)}$=15时,y取得最大值,此时y=1250,
∴售价降价15元时,最大销售利润是1250元.
点评 本题考查的是一元二次方程和二次函数的应用,根据题意找出等量关系列出方程和函数解析式是解题的关键,注意:解一元二次方程,得到两个根,检验两个根的合理性.

练习册系列答案
相关题目
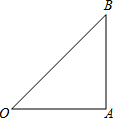 如图,Rt△ABC中,∠OAB=90°,OA=AB=2,
如图,Rt△ABC中,∠OAB=90°,OA=AB=2,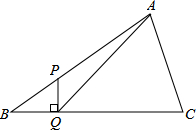 如图,在△ABC中,∠B=30°,点P是AB上一点,AP=3BP,PQ⊥BC于Q,连接AQ,则cos∠AQC的值为$\frac{3\sqrt{129}}{43}$.
如图,在△ABC中,∠B=30°,点P是AB上一点,AP=3BP,PQ⊥BC于Q,连接AQ,则cos∠AQC的值为$\frac{3\sqrt{129}}{43}$.
 如图,把△ABC绕B点逆时针方向旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC=77°.
如图,把△ABC绕B点逆时针方向旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC=77°.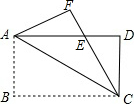 如图,将矩形ABCD沿对角线AC折叠,B点落在F,FC与AD交于E点,求证:ED=EF.
如图,将矩形ABCD沿对角线AC折叠,B点落在F,FC与AD交于E点,求证:ED=EF.