题目内容
15. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),如图,图中的折线表示y与x之间的函数关系,由图象可知:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),如图,图中的折线表示y与x之间的函数关系,由图象可知:(1)甲、乙两地之间的距离为900km;
(2)快车的速度为150km/h;
(3)线段BC对应的解析式为y=225x-900(4≤x≤6)(写自变量x的取值范围)
分析 (1)由函数图象可以直接求出甲乙两地之间的距离;
(2)由函数图象的数据,根据速度=路程÷时间就可以得出慢车的速度,由相遇问题求出速度和就可以求出快车的速度进而得出结论;
(3)由快车的速度求出快车走完全程的时间就可以求出点C的横坐标,由两车的距离=速度和×时间就可以求出C点的纵坐标,由待定系数法就可以求出结论.
解答 解:(1)由题意,得甲、乙两地之间的距为900km.
故答案为:900;
(2)由题意,得
快车与慢车的速度和为:900÷4=225km/h,
慢车的速度为:900÷12=75km/h,
快车的速度为:225-75=150 km/h.
故答案为:150;
(3)由题意,得快车走完全程的时间按为:900÷150=6h,
6时时两车之间的距离为:225×(6-4)=450km.
则C(6,450).
设线段BC的解析式为y=kx+b,由题意,得
$\left\{\begin{array}{l}{0=4k+b}\\{450=6k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=225}\\{b=-900}\end{array}\right.$,
则y=225x-900,自变量x的取值范围是4≤x≤6.
故答案为:y=225x-900(4≤x≤6).
点评 本题考查了行程问题的数量关系路程÷时间=速度的运用,待定系数法求一次函数的解析式的运用,相遇问题的数量关系的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.一次函数y=-2x+3的图象与x轴的交点坐标是( )
| A. | (0,3) | B. | (3,0) | C. | ($\frac{3}{2}$,0) | D. | ($\frac{2}{3}$,0) |
10.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外其它完全相同,小明通过多次摸球试验后发现其中摸到红色,黑色球的概率稳定在15%和40%,则口袋中白色球的个数很可能是( )
| A. | 25 | B. | 26 | C. | 29 | D. | 27 |
7.下列图形:任取一个既是轴对称图形又是中心对称图形的概率是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
5.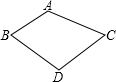 如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )
如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )
 如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )
如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )| A. | 90° | B. | 110° | C. | 120° | D. | 140° |
 如图,AD∥BE,∠EDC=∠C,∠A与∠E相等吗?并说明理由.
如图,AD∥BE,∠EDC=∠C,∠A与∠E相等吗?并说明理由. 解不等式组$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并将其解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并将其解集在数轴上表示出来.