题目内容
对于整数a,规定f(a)=
,例如:f(4)=
=
,f(
)=
=
,则f(2014)+f(2013)+…+f(2)+f(1)+f(1)+f(
)+…+f(
)+f(
)= .
| 1 |
| 1+a |
| 1 |
| 1+4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 | ||
1+
|
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2013 |
| 1 |
| 2014 |
考点:有理数的混合运算
专题:规律型
分析:由于f(a)=
,f(
)=
=
,则f(a)+f(
)=
+
=1,依此根据加法交换律两两结合,再相加即可求解.
| 1 |
| 1+a |
| 1 |
| a |
| 1 | ||
1+
|
| a |
| 1+a |
| 1 |
| a |
| 1 |
| 1+a |
| a |
| 1+a |
解答:解:∵f(a)=
,f(
)=
=
,
∴f(a)+f(
)=
+
=1,
∴f(2014)+f(2013)+…+f(2)+f(1)+f(1)+f(
)+…+f(
)+f(
)
=[f(2014)+f(
)]+[f(2013)+f(
)]+…+[f(2)+f(
)]+[f(1)+f(1)]
=1×2014
=2014.
故答案为:2014.
| 1 |
| 1+a |
| 1 |
| a |
| 1 | ||
1+
|
| a |
| 1+a |
∴f(a)+f(
| 1 |
| a |
| 1 |
| 1+a |
| a |
| 1+a |
∴f(2014)+f(2013)+…+f(2)+f(1)+f(1)+f(
| 1 |
| 2 |
| 1 |
| 2013 |
| 1 |
| 2014 |
=[f(2014)+f(
| 1 |
| 2014 |
| 1 |
| 2013 |
| 1 |
| 2 |
=1×2014
=2014.
故答案为:2014.
点评:考查了有理数的混合运算,关键是由规定得到f(a)+f(
)=
+
=1.
| 1 |
| a |
| 1 |
| 1+a |
| a |
| 1+a |

练习册系列答案
相关题目
 某小区的一所健身中心的平面图如图所示,活动区是面积为200m2的钜形,其长为20m,餐饮区是一个半圆形,面积为πm2,休息区是一个三角形,试判断此三角形的形状,并说明理由.
某小区的一所健身中心的平面图如图所示,活动区是面积为200m2的钜形,其长为20m,餐饮区是一个半圆形,面积为πm2,休息区是一个三角形,试判断此三角形的形状,并说明理由. 如图,在△ABC中,AB=BC,点D在AB的延长线上.
如图,在△ABC中,AB=BC,点D在AB的延长线上. 如图,在Rt△ABC中,∠BAC=90°,AB=AD,点D是AC的中点,将一块等腰直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
如图,在Rt△ABC中,∠BAC=90°,AB=AD,点D是AC的中点,将一块等腰直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.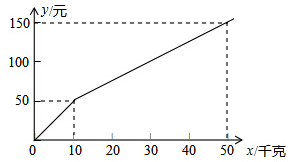 某种子公司以一定的价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不包含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(元)与一次购买种子数量x(千克)之间的函数关系如图所示
某种子公司以一定的价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不包含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(元)与一次购买种子数量x(千克)之间的函数关系如图所示