题目内容
8.化简:|a-$\sqrt{3}$|+|$\sqrt{2}$-a|分析 根据a的取值范围,先去绝对值再化简即可.
解答 解:当a$<\sqrt{2}$时,
原式=$\sqrt{3}$-a+$\sqrt{2}$-a
=$\sqrt{3}$+$\sqrt{2}$-2a;
当$\sqrt{2}$≤a<$\sqrt{3}$时,
原式=$\sqrt{3}$-a-$\sqrt{2}$+a=$\sqrt{3}$-$\sqrt{2}$;
当$\sqrt{3}$≤a时,
原式=a-$\sqrt{3}$-$\sqrt{2}$+a=-$\sqrt{3}$-$\sqrt{2}$+2a.
点评 此题主要考查与绝对值相关的运算,根据题意合理的针对a的取值进行分类讨论是解题的关键.

练习册系列答案
相关题目
13.把P1(2,$\sqrt{3}$)向下平移$\sqrt{3}$个单位长度再向左平移2个单位长度到达点P2处,则P2的坐标是( )
| A. | (4,0) | B. | (0,0) | C. | (2,2$\sqrt{3}$) | D. | (4,$\sqrt{3}$) |
 如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )



 端午节间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的方差=5.35.
端午节间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的方差=5.35.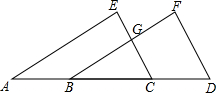 如图,已知:如图,EC∥FD,∠F=∠E,点A,B,C,D在一条直线上,EA与FB有怎样的位置关系?为什么?
如图,已知:如图,EC∥FD,∠F=∠E,点A,B,C,D在一条直线上,EA与FB有怎样的位置关系?为什么?