题目内容
14. 如图,若∠B=40°,A、C分别为角两边上的任意一点,连接AC,∠BAC与∠ACB的平分线交于点P1,则∠P1=110°,D、F也为角两边上的任意一点,连接DF,∠BFD与∠FDB的平分线交于点P2,…按这样规律,则∠P2016=110°.
如图,若∠B=40°,A、C分别为角两边上的任意一点,连接AC,∠BAC与∠ACB的平分线交于点P1,则∠P1=110°,D、F也为角两边上的任意一点,连接DF,∠BFD与∠FDB的平分线交于点P2,…按这样规律,则∠P2016=110°.
分析 根据三角形的内角和得到∠BAC+∠BCA=180°-∠B=140°,由角平分线的定义得到∠P1AC=$\frac{1}{2}$BAC,∠P1CA=$\frac{1}{2}$∠BCA,于是得到∠P1AC+∠P1CA=$\frac{1}{2}$(∠BAC+∠ACB)=70°,根据三角形的内角和得到∠P1=180°-(∠P1AC+∠P1CA)=110°,同理∠P2=110°按这样规律,则∠P2016=110°.
解答 解:∵∠B=40°,
∴∠BAC+∠BCA=180°-∠B=140°,
∵∠BAC与∠ACB的平分线交于P1,
∴∠P1AC=$\frac{1}{2}$BAC,∠P1CA=$\frac{1}{2}$∠BCA,
∴∠P1AC+∠P1CA=$\frac{1}{2}$(∠BAC+∠ACB)=70°,
∴∠P1=180°-(∠P1AC+∠P1CA)=110°,
同理∠P2=110°,…,
按这样规律,则∠P2016=110°,
故答案为:110°,110°.
点评 本题考查了三角形的内角和,角平分线的定义,熟练掌握三角形的内角和是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
5.下列式子不正确的是( )
| A. | ${2^{-1}}=\frac{1}{2}$ | B. | (-2)-2=4 | C. | ${({\frac{1}{2}})^{-3}}$=8 | D. | (-2)0=1 |
3.下列计算中,正确的是( )
| A. | (a2)3=a8 | B. | a8÷a4=a2 | C. | a3+a2=a5 | D. | a2•a3=a5 |
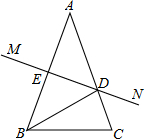 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.若∠DBC=33°,∠A的度数为38°.
如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.若∠DBC=33°,∠A的度数为38°.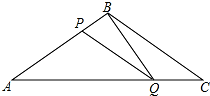 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.