题目内容
19.已知抛物线y=-$\frac{1}{6}{x}^{2}$+$\frac{3}{2}x+6$与x轴交于A,B两点,与y轴交于点C,若点D是AB的中点,求CD的长.分析 令y=0,则-$\frac{1}{6}$x2+$\frac{3}{2}$x+6=0,由此得到A、B两点坐标,由D为AB的中点,求出OD的长,x=0时,y=6,所以OC=6,根据勾股定理求出CD即可.
解答 解:当y=0,即-$\frac{1}{6}$x2+$\frac{3}{2}$x+6=0,解得:x1=-3,x2=12;
设A、B两点坐标分别为(-3,0)(12,0)
∵D为AB的中点,
∴D(4.5,0),
∴OD=4.5,
当x=0时,y=6,
∴OC=6,
由勾股定理,得:CD=$\sqrt{{6}^{2}+4.{5}^{2}}=\frac{15}{2}$.
点评 本题主要考查了二次函数与一元二次方程的关系和抛物线的对称性,求出AB中点D的坐标是解决问题的关键.

练习册系列答案
相关题目
10.等腰三角形的两边长分别为3和6,则第三边长是( )
| A. | 3 | B. | 6 | C. | 3,6 | D. | 9 |
14.设a为有理数,则|a|+a的结果( )
| A. | 可能是负数 | B. | 不可能是负数 | ||
| C. | 必定是正数 | D. | 可能是正数,也可能是负数 |
4.下列各式中,计算结果为正的是( )
| A. | (-50)+(+4) | B. | 2.7+(-4.5) | C. | (-$\frac{1}{3}$)+$\frac{2}{5}$ | D. | 0+(-$\frac{1}{3}$) |
9.下列运算正确的是( )
| A. | (-3)+(-4)=3+(-4)=-1 | B. | (-3)+(-4)=-3+4=1 | C. | (-3)-(-4)=-3+4=1 | D. | (-3)-(-4)=-3-4=-7 |
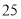 元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒
元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒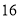 元,则该药品平均每次降价的百分率是_______.
元,则该药品平均每次降价的百分率是_______. 如图所示,AB=AC,BD=CE,AD=AE,求证:△ABE≌△ACD.
如图所示,AB=AC,BD=CE,AD=AE,求证:△ABE≌△ACD.