题目内容
设a,b,c是实数,若a+b+c=2
+4
+6
-14,求a(b+c)+b(c+a)+c(a+b)的值.
| a+1 |
| b+1 |
| c-2 |
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:根据已知条件求出(
-1)2+(
-2)2+(
-3)2=0,从而得出a=0,b=3,c=11,再代入计算即可.
| a+1 |
| b+1 |
| c-2 |
解答:解:∵a+b+c=2
+4
+6
-14,
∴a+b+c-2
-4
-6
+14=0,
∴(
)2-2
+1+(
)2-4
+4+(
)2-6
+9=0,
∴(
-1)2+(
-2)2+(
-3)2=0,
∴
-1=0,
-2=0,
-3=0,
∴a=0,b=3,c=11,
∴a(b+c)+b(c+a)+c(a+b)=0+3×11+11×3=66.
| a+1 |
| b+1 |
| c-2 |
∴a+b+c-2
| a+1 |
| b+1 |
| c-2 |
∴(
| a+1 |
| a+1 |
| b+1 |
| b+1 |
| c-2 |
| c-2 |
∴(
| a+1 |
| b+1 |
| c-2 |
∴
| a+1 |
| b+1 |
| c-2 |
∴a=0,b=3,c=11,
∴a(b+c)+b(c+a)+c(a+b)=0+3×11+11×3=66.
点评:此题考查了配方法的应用,关键是通过配方,根据非负数的性质求出a=0,b=3,c=11.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知?ABCD的对角线AC,BD交于点O,E,F分别是OA,OC的中点.
如图,已知?ABCD的对角线AC,BD交于点O,E,F分别是OA,OC的中点.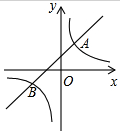 如图,直线y=x+2与双曲线y=
如图,直线y=x+2与双曲线y=
 如图,∠A=10°,∠ABC=90°,∠ACB=∠DCE,∠ADC=∠EDF,∠CED=∠FEG.则∠ACB=
如图,∠A=10°,∠ABC=90°,∠ACB=∠DCE,∠ADC=∠EDF,∠CED=∠FEG.则∠ACB=