题目内容
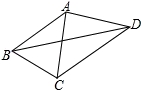
如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为__________．
88°．
【考点】圆周角定理．
【分析】由AB=AC=AD，可得B，C，D在以A为圆心，AB为半径的圆上，然后由圆周角定理，证得∠CAD=2∠CBD，∠BAC=2∠BDC，继而可得∠CAD=2∠BAC．
【解答】解：∵AB=AC=AD，
∴B，C，D在以A为圆心，AB为半径的圆上，
∴∠CAD=2∠CBD，∠BAC=2∠BDC，
∵∠CBD=2∠BDC，∠BAC=44°，
∴∠CAD=2∠BAC=88°．
故答案为：88°．
【点评】此题考查了圆周角定理．注意得到B，C，D在以A为圆心，AB为半径的圆上是解此题的关键．
练习册系列答案
阶梯计算系列答案
相关题目
，
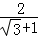的式子，其实我们还可以将其进一步变形：
=
；
=
=
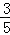
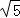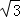﹣1．
=
=
=
﹣
=
=
=
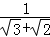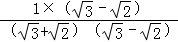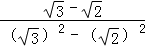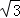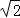
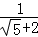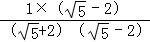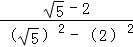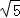﹣2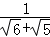
=__________；
=__________；
=__________．
+
+
+…+
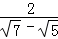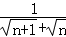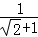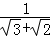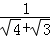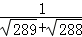（写出解答过程）
DO，连接AD、BC交于点P，考察下列结论，其中正确的是( )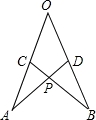
____ （用含有n的代数式表示）．
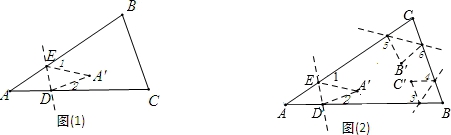
AC=CD．