Question

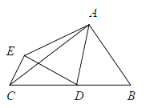
【题目】如图，已知∠MON＝90°，A是∠MON内部的一点，过点A作AB⊥ON，垂足为点B，AB＝3厘米，OB＝4厘米，动点E，F同时从O点出发，点E以1.5厘米/秒的速度沿ON方向运动，点F以2厘米/秒的速度沿OM方向运动，EF与OA交于点C，连接AE，当点E到达点B时，点F随之停止运动．设运动时间为t秒（t＞0）．

（1）当t＝1秒时，△EOF与△ABO是否相似？请说明理由；

（2）在运动过程中，不论t取何值时，总有EF⊥OA．为什么？

（3）连接AF，在运动过程中，是否存在某一时刻t，使得S△AEF＝S四边形AEOF？若存在，请求出此时t的值；若不存在，请说明理由．

Answer 1

【答案】（1）相似，理由见解析；（2）见解析；（3）存在，t＝，理由见解析

【解析】

（1）依据两组对边成比例及夹角相等，得出△EOF∽△ABO．

（2）通过证明Rt△EOF∽Rt△ABO，依据相似三角形的对应角相等，结合等量代换，及三角形外角的性质，即可证明EF⊥OA．

（3）根据S△AEF＝S梯形ABOF﹣S△FOE﹣S△ABE以及S四边形AEOF＝S梯形ABOF﹣S△ABE计算出S△AEF与S四边形AEOF，根据已知条件写出关于t的方程，进而可求出t的值．

解：（1）∵t＝1，

∴OE＝1.5厘米，OF＝2厘米，

又∵AB＝3厘米，OB＝4厘米，

∴

又∵∠MON＝∠ABE＝90°，

∴△EOF∽△ABO．

（2）在运动过程中，OE＝1.5t，OF＝2t．

又∵AB＝3，OB＝4．

∴．

又∵∠EOF＝∠ABO＝90°，

∴Rt△EOF∽Rt△ABO．

∴∠AOB＝∠EFO．

又∵∠AOB+∠FOC＝90°，

∴∠EFO+∠FOC＝90°，

∴EF⊥OA．

（3）如图，连接AF，

∵OE＝1.5t，OF＝2t，

∴BE＝4﹣1.5t

∴S△FOE＝OEOF＝×1.5t×2t＝t2，

S△ABE＝×（4﹣1.5t）×3＝6﹣t，

S梯形ABOF＝（2t+3）×4＝4t+6，

∴S△AEF＝S梯形ABOF﹣S△FOE﹣S△ABE＝4t+6﹣t2﹣（6﹣t）＝﹣t2+t，

S四边形AEOF＝S梯形ABOF﹣S△ABE＝4t+6﹣（6﹣t）＝t，

又∵S△AEF＝S四边形AEOF

∴﹣t2+t＝×t，（0＜t＜）

解得t＝或t＝0（舍去）．

∴当t＝时，S△AEF＝S四边形AEOF．