Question

已知线段AB=10，作直线AB上有一点C，且BC=6，M为线段AC的中点，则线段AM的长为（　　）

A．4

B．8

C．2或8

D．4或8

Answer 1

分析：根据题意画出符合条件的两种情况，求出AC的长，根据AM=

1

2

AC求出即可．

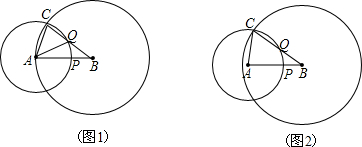
解答：解：当点C在线段AB上时，如图1所示，
∵AB=10cm，BC=6cm，
∴AC=AB-BC=10-6=4cm，
∵M是AC的中点，
∴AM=

1

2

AC，
∴AM=

1

2

×4cm=2cm；
当点C在线段AB的延长线上时，如图2，
∵AB=10cm，BC=6cm，
∴AC=AB+BC=16cm，
∵M是AC的中点，
∴AM=

1

2

AC，
∴AM=

1

2

×16cm=8cm，
∴线段AM的长为2cm或8cm．
故选C．

点评：本题考查了两点间的距离，在求解没有图形的几何题时，应根据题意画图，同时注意图形的多样性，以免漏解．