题目内容
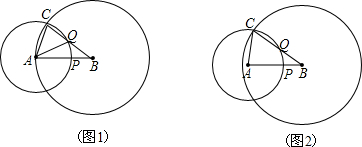
已知线段AB=10,点P在线段AB上,且AP=6,以A为圆心AP为半径作⊙A,点C在⊙A上,以B为圆心BC为半径作⊙B,射线BC与⊙A交于点Q(不与点C重合).(1)当⊙B过点A时(如图1),求CQ的长;
(2)当点Q在线段BC上时(如图2),设BC=x,CQ=y,试求y关于x的函数关系式,并写出定义域;
(3)当由A、P、Q、C四点构成的四边形是梯形时,求BC的长.
分析:(1)已知了两个圆的半径长,可通过证△CAQ∽△CBA,根据得到的比例线段即可求得CQ的长.
(2)过A作AH⊥BC于H,由于AC=AQ,根据等腰三角形的性质可得到CH、QH的长,在Rt△AQH和Rt△ABH中,分别用勾股定理表示出AH2,联立两式即可得到y、x的函数关系式.
(3)此题要分两种情况考虑:
①点A、Q在⊙B内部时,若四边形APQC是梯形,则PQ∥AC,在(2)题已求得CQ即y的表达式,可根据平行线分线段成比例定理,列式求得x的值;
②当A、Q在⊙B外部时,若四边形APCQ是梯形,则AQ∥PC,可仿照(2)的方法,过A作AH⊥BQ于H,求得QH的表达式,即可得到CQ的长,然后根据平行线分线段成比例定理,即可列式求得x的值.
(2)过A作AH⊥BC于H,由于AC=AQ,根据等腰三角形的性质可得到CH、QH的长,在Rt△AQH和Rt△ABH中,分别用勾股定理表示出AH2,联立两式即可得到y、x的函数关系式.
(3)此题要分两种情况考虑:
①点A、Q在⊙B内部时,若四边形APQC是梯形,则PQ∥AC,在(2)题已求得CQ即y的表达式,可根据平行线分线段成比例定理,列式求得x的值;
②当A、Q在⊙B外部时,若四边形APCQ是梯形,则AQ∥PC,可仿照(2)的方法,过A作AH⊥BQ于H,求得QH的表达式,即可得到CQ的长,然后根据平行线分线段成比例定理,即可列式求得x的值.
解答:解:(1)∵C、Q在⊙A上,
∴AC=AQ,∴∠C=∠AQC,
∵⊙B过A、C,
∴BA=BC,∴∠C=∠CAB,
∴∠AQC=∠CAB,
∵∠C=∠C,
∴△CAQ∽△CBA,(1分)
∴AC2=CQ•CB,(1分)
即62=10•CQ,
∴CQ=3.6.(2分)
(2)作AH⊥CQ,则QH=CH=
,(1分)
 且AQ2-QH2=AB2-BH2;(1分)
且AQ2-QH2=AB2-BH2;(1分)
∵BH=x-
,且AQ=6,∴36-
=100-(x-
)2
解之得:y=
;(8<x≤16)
(3)当Q在BC上时:如图1
A、P、Q、C四点构成的四边形是梯形,
且AC∥PQ,则
=
∵CQ=y=
,CB=x,AP=6,
∴
=
,
∵x>0,
∴解得:x=4
;(2分)
当Q在BC延长线上时:如图2
 A、P、Q、C四点构成的四边形是梯形,
A、P、Q、C四点构成的四边形是梯形,
且AQ∥PC,则
=
,
作AH⊥CQ,则QH=CH,且AQ2-QH2=AB2-BH2
即36-QH2=100-(x-QH)2,得QH=
,
则CQ=
,(1分)
则
=
,
∵x>0,
∴解得:x=
,(2分)
∴当A、P、Q、C四点构成的四边形是梯形时,BC的长为4
或
.
∴AC=AQ,∴∠C=∠AQC,
∵⊙B过A、C,
∴BA=BC,∴∠C=∠CAB,
∴∠AQC=∠CAB,
∵∠C=∠C,
∴△CAQ∽△CBA,(1分)
∴AC2=CQ•CB,(1分)
即62=10•CQ,
∴CQ=3.6.(2分)
(2)作AH⊥CQ,则QH=CH=
| y |
| 2 |
 且AQ2-QH2=AB2-BH2;(1分)
且AQ2-QH2=AB2-BH2;(1分)∵BH=x-
| y |
| 2 |
| y2 |
| 4 |
| y |
| 2 |
解之得:y=
| x2-64 |
| x |
(3)当Q在BC上时:如图1

A、P、Q、C四点构成的四边形是梯形,
且AC∥PQ,则
| BA |
| AP |
| BC |
| CQ |
∵CQ=y=
| x2-64 |
| x |
∴
| 10 |
| 6 |
| x | ||
|
∵x>0,
∴解得:x=4
| 10 |
当Q在BC延长线上时:如图2
 A、P、Q、C四点构成的四边形是梯形,
A、P、Q、C四点构成的四边形是梯形,且AQ∥PC,则
| BP |
| AP |
| BC |
| CQ |
作AH⊥CQ,则QH=CH,且AQ2-QH2=AB2-BH2
即36-QH2=100-(x-QH)2,得QH=
| 64-x2 |
| 2x |
则CQ=
| 64-x2 |
| x |
则
| 4 |
| 6 |
| x | ||
|
∵x>0,
∴解得:x=
| 8 |
| 5 |
| 10 |
∴当A、P、Q、C四点构成的四边形是梯形时,BC的长为4
| 10 |
| 8 |
| 5 |
| 10 |
点评:本题考查了相似三角形的判定和性质、勾股定理、平行线分线段成比例定理等知识,注意(3)题要根据A、Q的不同位置分类讨论,不要漏解.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
 (2013•桂林)如图,已知线段AB=10,AC=BD=2,点P是CD上一动点,分别以AP、PB为边向上、向下作正方形APEF和PHKB,设正方形对角线的交点分别为O1、O2,当点P从点C运动到点D时,线段O1O2中点G的运动路径的长是
(2013•桂林)如图,已知线段AB=10,AC=BD=2,点P是CD上一动点,分别以AP、PB为边向上、向下作正方形APEF和PHKB,设正方形对角线的交点分别为O1、O2,当点P从点C运动到点D时,线段O1O2中点G的运动路径的长是 已知线段AB=10,如图,若C为线段AB的中点,D在线段CB上,DA=6,DB=4,则CD的长度是
已知线段AB=10,如图,若C为线段AB的中点,D在线段CB上,DA=6,DB=4,则CD的长度是