题目内容
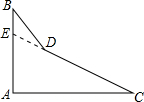一个零件的形状如图所示，零件要求∠A必须等于90°，∠B和∠C分别为45°和35°，检验工人量得∠BDC=159°，断定这个零件不合格，下面是一位同学的解法：解：延长CD交AB于E，∠EDC=∠B+∠BED=∠B+∠A+∠C=170°，而量得∠BDC=159°，因为170°≠159°，所以零件不合格，请问这位同学的解答正确吗？你能再找一种方法来检验吗？考点：三角形的外角性质,三角形内角和定理
专题：应用题
分析：根据三角形外角的性质可知这位同学的解答正确．延长BD交AC于点E，再由三角形外角的性质求出∠DEC的度数，进而得出∠BDC的度数，再与已知∠BDC=159°相比较即可．
解答：
解：正确．
延长BD交AC于点E，
∵∠DEC是△ABE的外角，∠A=90°，∠B=45°，
∴∠DEC=90°+45°=135°．
∵∠BDC是△CDE的外角，∠C=35°，
∴∠BDC=∠DEC+∠C=135°+35°=170°≠159°，
∴此零件不合格．
解：正确．延长BD交AC于点E，
∵∠DEC是△ABE的外角，∠A=90°，∠B=45°，
∴∠DEC=90°+45°=135°．
∵∠BDC是△CDE的外角，∠C=35°，
∴∠BDC=∠DEC+∠C=135°+35°=170°≠159°，
∴此零件不合格．
点评：本题考查的是三角形的外角，熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
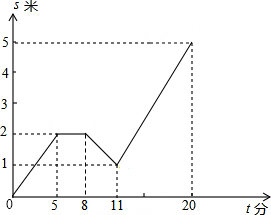一个水池，装有一个进水管和一个出水管，两个水管同时开放，水池内水位高为S（单位：米）与注水时间t（单位：分）之间的函数关系图象如图所示，下列四种说法：