题目内容
已知一个正比例函数与一个一次函数的图象交于点A(3,4),且一次函数的图象过点B,点B在x轴上,且AO=BO.
(1)求两个函数的解析式;
(2)求△AOB的面积.
(1)求两个函数的解析式;
(2)求△AOB的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据A的坐标先求出正比例函数的解析式,再根据已知条件求出点B的坐标,进而可得一次函数解析式;
(2)根据A、B的坐标即可求得三角形的底边长和高,从而求出三角形AOB的面积.
(2)根据A、B的坐标即可求得三角形的底边长和高,从而求出三角形AOB的面积.
解答: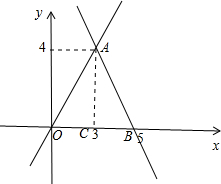 解:(1)如图,过A作AC⊥x轴于C点,
解:(1)如图,过A作AC⊥x轴于C点,
∵A(3,4),
∴AC=4,OC=3,
∴OA=5=OB
∴B(5,0),
设正比例函数的解析式为y=mx,
∵正比例函数的图象过A(3,4)
∴4=3m,m=
,
∴正比例函数的解析式为y=
x;
设一次函数的解析式为y=kx+b,
∵过A(3,4)、B(5,0)
∴
.
解得:
.
∴一次函数的解析式为y=-2x+10,
(2)∵A(3,4),B(5,0),
∴三角形AOB的面积为5×4×
=10.
 解:(1)如图,过A作AC⊥x轴于C点,
解:(1)如图,过A作AC⊥x轴于C点,∵A(3,4),
∴AC=4,OC=3,
∴OA=5=OB
∴B(5,0),
设正比例函数的解析式为y=mx,
∵正比例函数的图象过A(3,4)
∴4=3m,m=
| 4 |
| 3 |
∴正比例函数的解析式为y=
| 4 |
| 3 |
设一次函数的解析式为y=kx+b,
∵过A(3,4)、B(5,0)
∴
|
解得:
|
∴一次函数的解析式为y=-2x+10,
(2)∵A(3,4),B(5,0),
∴三角形AOB的面积为5×4×
| 1 |
| 2 |
点评:主要考查了用待定系数法解函数解析式和一次函数图象的性质,还考查了学生的分析能力和读图能力.

练习册系列答案
相关题目
已知关于x的方程(2a+1)x=a-1有解,那么a应满足的是( )
| A、a≠0 | ||
B、a≠
| ||
C、a≠-
| ||
D、a=
|
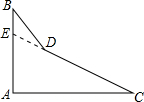 一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,断定这个零件不合格,下面是一位同学的解法:解:延长CD交AB于E,∠EDC=∠B+∠BED=∠B+∠A+∠C=170°,而量得∠BDC=159°,因为170°≠159°,所以零件不合格,请问这位同学的解答正确吗?你能再找一种方法来检验吗?
一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,断定这个零件不合格,下面是一位同学的解法:解:延长CD交AB于E,∠EDC=∠B+∠BED=∠B+∠A+∠C=170°,而量得∠BDC=159°,因为170°≠159°,所以零件不合格,请问这位同学的解答正确吗?你能再找一种方法来检验吗?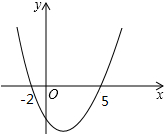 已知二次函数y=ax2-4x+c的图象如图所示.
已知二次函数y=ax2-4x+c的图象如图所示.